在正方形ABCD中，對角線AC=12，點E、F在AC上．
（1）如圖1，若AE=CF，求證：BE=BF；
（2）如圖2，若AE=3，∠EBF=45°，求CF的長；
（3）如圖3，若AE=4，F是AC的中點，點P在AB邊上從點A開始向點B運動，在此過程中設PE+PF=a,則實數a的取值范圍是 213≤a≤210+6213≤a≤210+6，使a為整數時點P的個數為 8個8個．
13
10
13
10
【考點】四邊形綜合題．
【答案】2≤a≤2+6；8個
13
10
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/25 8:0:9組卷：531引用：1難度：0.3
相似題
-
1．（1）問題發現：如圖①，正方形AEFG的兩邊分別在正方形ABCD的邊AB和AD上，連接CF．
①寫出線段CF與DG的數量關系 ；
②寫出直線CF與DG所夾銳角的度數 ．
（2）拓展探究：
如圖②，將正方形AEFG繞點A逆時針旋轉，在旋轉的過程中，（1）中的結論是否仍然成立？請利用圖②進行說明．
（3）問題解決
如圖③，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC=4，O為AC的中點．點D在直線BC上運動，連接OE，則在點D的運動過程中，求線段OE的長的最小值．（直接寫出結果）
發布：2025/6/2 23:30:2組卷：143引用：1難度：0.1 -
2．已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=BC．
（1）如圖1．連接BD，若∠BAD=90°，求證：AD=CD．
（2）如圖2，點P，Q分別在線段AD，DC上，滿足PQ=AP+CQ，求證：∠PBQ=∠ABP+∠QBC；
（3）若點Q在DC的延長線上，點P在DA的延長線上，如圖3所示，仍然滿足PQ=AP+CQ，請寫出∠PBQ與∠ADC的數量關系，并給出證明過程．
發布：2025/6/3 0:0:1組卷：434引用：2難度：0.3 -
3．（1）發現；如圖1，在等腰直角三角形ABC中，∠ACB=90°，點F為BC上一點，以BF為邊作正方形BFED，點E在AB上，若AC=BC=2，
，則BF=2=；AECF
（2）探究：如圖2，在（1）的條件下，將正方形BFED繞點B旋轉，連接AE，CF，求的值；AECF
（3）拓展：在（2）的條件下，當A，E，F三點共線時候，直接寫出線段CF的長．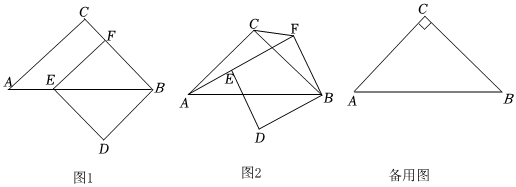
發布：2025/6/2 23:30:2組卷：29引用：1難度：0.2