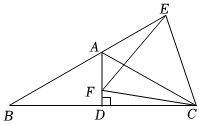
如圖，等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于點D，點E在BA的延長線上，點F在線段AD上，且EF=FC．有下面四個結論：
（1）AB=2AD；
（2）△AEF≌△ACF；
（3）△EFC是等邊三角形；
（4）FA+AE=EC．
其中所有正確結論的序號是 （1）（3）（1）（3）．
【考點】三角形綜合題．
【答案】（1）（3）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 21:0:1組卷：210引用：2難度：0.5
相似題
-
1．對于平面直角坐標系xOy中的線段MN及點Q，給出如下定義：
若點Q滿足QM=QN，則稱點Q為線段MN的“中垂點”；當QM=QN=MN時，稱點Q為線段MN的“完美中垂點”．
（1）如圖1，A（4，0），下列各點中，線段OA的中垂點是 ．
Q1（1，4），Q2（4，），Q3（2，-2）3
（2）如圖2，點A為x軸上一點，若Q（1，）為線段OA的“完美中垂點”，∠QOA=60°寫出線段OQ的兩個“完美中垂點”是 和 ．3
（3）如圖3，若點A為x軸正半軸上一點，點Q為線段OA的“完美中垂點”，點P（0，m）在y軸負半軸上，在線段PA上方畫出線段AP的“完美中垂點”M，直接寫出MQ=．（用含m的式子表示）．并求出∠MQA．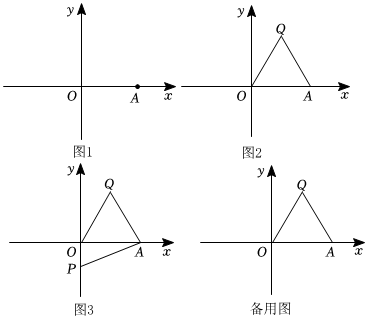
發布：2025/6/1 3:0:1組卷：228引用：2難度：0.3 -
2．如圖，已知A（a,b），AB⊥y軸交y軸于點B，且滿足
+（b-2022）2=0．a-2022
（1）求A點坐標；
（2）分別以AB，AO為邊作等邊三角形△ABC和△AOD，如圖1，試判定線段AC和DC的數量關系和位置關系，并說明理由；
（3）如圖2，過點A作AE⊥x軸交x軸于點E，點F，G分別為線段OE，AE上的兩個動點，滿足∠FBG=45°，設OF=a,AG=b,FG=c,試證明：．1a+1b=cab
發布：2025/6/1 3:30:2組卷：690引用：3難度：0.6 -
3．如圖，在△ABC中，∠BAC=90°；點D、點E分別在線段AB、線段AC上，連接CD、DE，且∠EDC=45°；過E點作DE的垂線EF，交BA延長線于點H，交CD于點F，交BC于點G．
（1）如圖1，若CE=2AD，AD=2AE=4，求CD的長；
（2）如圖2，若FH=EG，求證：BH=BG；
（3）如圖3，在（2）的條件下，點M是BC邊上的一個動點，以線段MC為邊，在直線BC下方作等邊△CMN，連接AM、AN；當ED=BD，AH=2時，請直接寫出在M的運動過程中AM+AN取得的最小值．發布：2025/6/1 4:0:1組卷：591引用：1難度：0.1