對于平面直角坐標系xOy中的線段MN及點Q，給出如下定義：
若點Q滿足QM=QN，則稱點Q為線段MN的“中垂點”；當QM=QN=MN時，稱點Q為線段MN的“完美中垂點”．
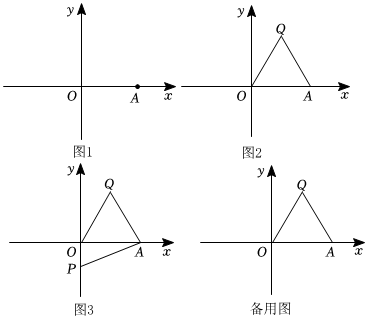
（1）如圖1，A（4，0），下列各點中，線段OA的中垂點是 Q3（2，-2）Q3（2，-2）．
Q1（1，4），Q2（4，3），Q3（2，-2）
（2）如圖2，點A為x軸上一點，若Q（1，3）為線段OA的“完美中垂點”，∠QOA=60°寫出線段OQ的兩個“完美中垂點”是 （2，0）（2，0）和 （-1，3）（-1，3）．
（3）如圖3，若點A為x軸正半軸上一點，點Q為線段OA的“完美中垂點”，點P（0，m）在y軸負半軸上，在線段PA上方畫出線段AP的“完美中垂點”M，直接寫出MQ=-m-m．（用含m的式子表示）．并求出∠MQA．
3
3
3
3
【考點】三角形綜合題．
【答案】Q3（2，-2）；（2，0）；（-1，）；-m
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/1 3:0:1組卷：228引用：2難度：0.3
相似題
-
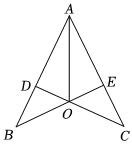1．如圖，AB=AC，CD⊥AB，BE⊥AC，垂足分別為D、E，BE、CD相交于點O，連接AO．
（1）不添加任何輔助線，寫出圖中所有的全等三角形．
（2）觀察猜想，AO是不是∠BAC的角平分線？如果認為是，請證明；如果認為不是，請說明理由．
（3）連接BC，如果OA=OB，求證：△ABC為等邊三角形．發布：2025/6/2 15:30:1組卷：19引用：1難度：0.3 -
2．在Rt△ABC中，∠ACB=90°，CD⊥AB于點D，E為AB上一點（不與A，B重合）
（1）如圖1，若BC=BE，求證：CE平分∠ACD；
（2）如圖2，若AC=BC，過點B作BF⊥CE于點F，交CD于G．
①求證：AE=CG；
②當BC=BE時，BG與CF的數量關系是．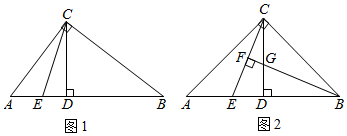
發布：2025/6/2 16:0:1組卷：409引用：2難度：0.4 -
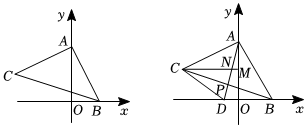3．如圖1，在平面直角坐標系中，點A在y軸上，點B在x軸上，以AB為邊作等腰直角三角形ABC，使AB=AC，∠BAC=90°，點C在第二象限．
（1）若點A（0，a），B（b,0），且a、b滿足+b2-6b+9=0，則a=，b=，點C的坐標為；a-6
（2）如圖2，過點C作CM⊥y軸于點M，AD平分∠BAC，交x軸于點D，交CM于點N，交BC于點P，求證：CP垂直平分DN：
（3）試探究（2）中OM，OD與MN之間的關系，并說明理由．發布：2025/6/2 16:30:2組卷：63引用：1難度：0.1