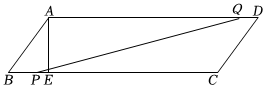
如圖，在?ABCD中，AB=15，BC=27，AE⊥BC于點E，且BE=9．點P從點B出發(fā)，沿BC以每秒3個單位長度的速度向終點C運動；點Q從點D出發(fā)，沿DA以每秒2個單位長度的速度向終點A運動，P、Q兩點同時出發(fā)，當點P停止時，點Q也隨之停止，連接PQ．設點P運動的時間為t秒（t＞0）．
（1）AE的長是 1212；
（2）用含t的代數(shù)式表示PE的長；
（3）設△QPE面積為S，求S關(guān)于t的函數(shù)關(guān)系式；
（4）當以E、D、P、Q為頂點的四邊形是平行四邊形時，直接寫出t的值．
【考點】四邊形綜合題．
【答案】12
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/6/3 22:30:1組卷：175引用：3難度：0.1
相似題
-
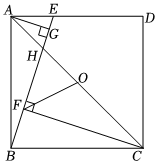1．如圖，在正方形ABCD中，O是AC的中點，E是AD上一點，連接BE，交AC于點H，作CF⊥BE于點F，AG⊥BE于點G，連接OF．
（1）求證：AG=BF；
（2）請找出線段FG與OF的數(shù)量關(guān)系并證明；
（3）證明：FH2+HG2=2OH2．發(fā)布：2025/6/5 16:30:2組卷：163引用：1難度：0.3 -
2．閱讀理解
材料一：一組對邊平行，另一組對邊不平行的四邊形叫梯形，其中平行的兩邊叫梯形的底邊，不平行的兩邊叫梯形的腰，連接梯形兩腰中點的線段叫梯形的中位線．梯形的中位線具有以下性質(zhì)：
梯形的中位線平行于兩底，并且等于兩底和的一半．
如圖（1）：在梯形ABCD中：AD∥BC
∵E、F是AB、CD的中點
∴EF∥AD∥BC
EF=（AD+BC）12
材料二：經(jīng)過三角形一邊的中點與另一邊平行的直線必平分第三邊
如圖（2）：在△ABC中：
∵E是AB的中點，EF∥BC
∴F是AC的中點
請你運用所學知識，結(jié)合上述材料，解答下列問題．
如圖（3）在梯形ABCD中，AD∥BC，AC⊥BD于O，E、F分別為AB、CD的中點，∠DBC=30°
（1）求證：EF=AC；
（2）若OD=3，OC=5，求MN的長．3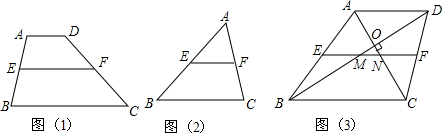
發(fā)布：2025/6/5 16:30:2組卷：635引用：5難度：0.5 -
3．市一中某數(shù)學興趣小組利用正方形硬紙片開展了一次活動，請認真閱讀下面的探究片段，完成提出的問題．四邊形ABCD是邊長為3的正方形，點E是射線BC上的動點，∠AEF=90°，且EF交正方形外角的平分線CF于點F．【探究1】當點E是BC中點時，如圖1，發(fā)現(xiàn)AE=EF，這需要證明AE與EF所在的兩個三角形全等，但△ABE與△FCE顯然不全等，考慮到點E是BC的中點，取AB的中點H，連接EH，證明△AHE與△ECF全等即可．（無需證明）
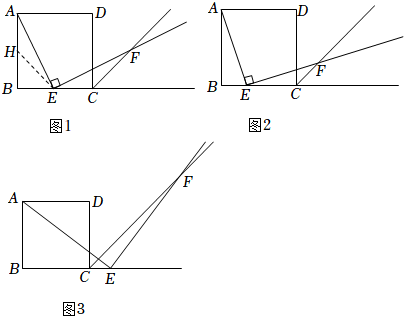
【探究2】（1）如圖2，如果把“點E是BC的中點”改成“點E是邊BC上（不與點B、C重合）的任意一點”，其他條件不變，那么結(jié)論“AE=EF”仍然成立嗎？如果成立，寫出證明過程，如果不成立，也請說明理由．
（2）如圖3，如果點E是邊BC延長線上的任意一點，其他條件不變，請你畫出圖象，并判斷“AE=EF”是否成立？（填“是”或“否”），如果是，請簡述一下輔助線的作法；如果否，也請說明理由．
【探究3】連接AF交直線CD于點I，連接EI，試探究線段BE，EI，ID之間的數(shù)量關(guān)系，請在備用圖中作出圖形并直接寫出結(jié)論．
【探究4】當CE=2時，此時△EIF的面積為 ．發(fā)布：2025/6/5 17:30:1組卷：433引用：2難度：0.1