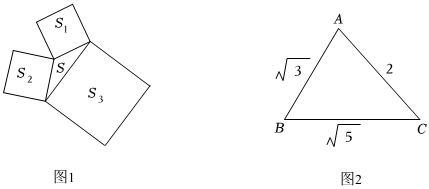
海倫是古希臘數學家，約公元62年左右活躍于亞歷山大，年青時海倫酷愛數學，他的代表作《量度論》主要是研究面積、體積和幾何分比問題，其中一段探究三角形面積的方法翻譯如下：如圖1，設三角形面積為S，以三角形各邊為邊向外作正方形，三個正方形的面積分別記作S1、S2、S3，定義：S=S1+S2+S32；S1'=S-S1；S2'=S-S2；S3'=S-S3；FS=S1'×S2′+S2'×S3'+S3'×S1'，經研究發現，FS=4S2．如：三角形三條邊分別為13、14、15，則S1=169，S2=196，S3=225，S=295，S1'=126；S2′=99；S3′=70；Fs=28224，所以S2=28224÷4=7056=842，故三角形的面積S=84．
（1）如圖2，在△ABC中，S1=3，S2=4，S3=5，則S=66，Fs=1111，△ABC的面積S=112112．
（2）在△DEF中，若S1′=x-3；S2′=x+3；S3′=5-x.
①若△DEF的面積S=3，求x的值；
②若△DEF的面積是否存在最大值？如果存在，請直接寫出此時外接圓的直徑，如果不存在，請簡要說明理由．
S
=
S
1
+
S
2
+
S
3
2
S
S
S
S
S
11
2
11
2
3
【答案】6；11；
11
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/26 17:0:2組卷：60引用：1難度：0.7
相似題
-
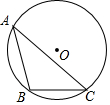1．如圖，⊙O是△ABC的外接圓，BC=2，∠BAC=30°，則⊙O的直徑長等于．發布：2025/5/22 1:30:1組卷：634引用：9難度：0.6 -
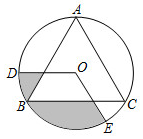2．如圖，等邊三角形ABC內接于⊙O，點D，E是⊙O上兩點，且∠DOE=120°，若OD=2，則圖中陰影部分的面積為．發布：2025/5/22 2:30:1組卷：165引用：3難度：0.5 -
3．如圖，在△ABC中，AC=BC．D是AB上一點，⊙O經過點A，C，D交BC于點E．過點D作DF∥BC，分別交AC于點G，⊙O于點F．
（1）求證AC=DF；
（2）若AC=10，AB=12，CF=3，求BE的長．發布：2025/5/22 4:30:1組卷：1465引用：3難度：0.4