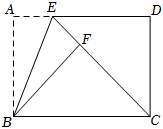
如圖，長方形ABCD中，∠A=∠ABC=∠BCD=∠D=90°，AB=CD=3，AD=BC=5，點E為射線AD上的一個動點，△ABE與△FBE關于直線BE對稱，當點E、F、C三點共線時，AE的長為 1或91或9．
【答案】1或9
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/14 15:30:1組卷：713引用：2難度：0.4
相似題
-
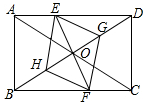1．已知：如圖，在矩形ABCD中，點E在邊AD上，點F在邊BC上，且AE=CF，作EG∥FH，分別與對角線BD交于點G、H，連接EH，FG．
（1）求證：△BFH≌△DEG；
（2）連接DF，若BF=DF，則四邊形EGFH是什么特殊四邊形？證明你的結論．發布：2025/6/15 7:30:2組卷：2286引用：14難度：0.5 -
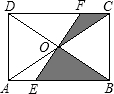2．如圖，在矩形ABCD中，對角線AC、BD相交于點O，過O的直線EF分別交AB、CD于點E、F．若圖中陰影部分的面積為6，則矩形ABCD的面積為（ ）發布：2025/6/15 7:30:2組卷：396引用：10難度：0.7 -
3．如圖，矩形ABCD中，對角線AC，BD相交于點O，下列結論不一定成立的是（ ）發布：2025/6/15 8:0:1組卷：422引用：2難度：0.8