舊知新意：
我們容易證明，三角形的一個外角等于與它不相鄰的兩個內角的和，那么，三角形的一個內角與它不相部的兩個外角的和之間存在怎樣的數量關系呢？
嘗試探究：
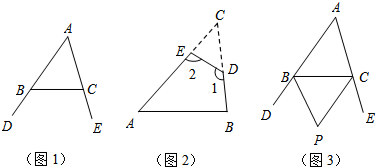
（1）如圖1，∠DBC與∠ECB分別為△ABC的兩個外角，試探究∠A與∠DBC+∠ECB之間存在怎樣的數量關系？為什么？
初步應用：
（2）如圖2，在△ABC紙片中剪去△CDE，得到四邊形ABDE，∠1=130°，則∠2-∠C=50°50°；
（3）小明聯想到了曾經解決的一個問題：如圖3，在△ABC中，BP、CP分別平分外角∠DBC、∠ECB，∠P與∠A有何數量關系（直接寫出結論）．
【答案】50°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：169引用：4難度：0.5
相似題
-
1．將一正方形紙片按下列順序折疊，然后將最后折疊的紙片沿虛線剪去上方的小三角形．將紙片展開，得到的圖形是（ ）
發布：2025/6/19 1:0:1組卷：1050引用：97難度：0.5 -
2．如圖所示，如果將矩形紙沿虛線①對折后，沿虛線②剪開，剪出一個直角三角形，展開后得到一個等腰三角形，則展開后的等腰三角形周長是（ ）
發布：2025/6/23 20:0:1組卷：209引用：35難度：0.9 -
3．將一張長與寬之比為
的矩形紙片ABCD進行如下操作：對折并沿折痕剪開，發現每一次所得到的兩個矩形紙片長與寬之比都是2（每一次的折痕如圖中的虛線所示）．已知AB=1，則第3次操作后所得到的其中一個矩形紙片的周長是；第2020次操作后所得到的其中一個矩形紙片的周長是．2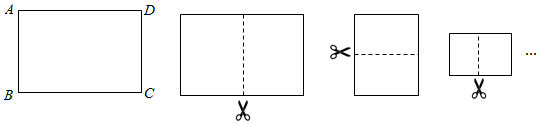
發布：2025/6/20 1:30:2組卷：49引用：1難度：0.4