已知拋物線y=-x2+bx+c與直線y=-4x+m相交于第一象限不同的兩點，A（5，n），B（e,f）
（1）若點B的坐標(biāo)為（3，9），求此拋物線的解析式；
（2）將此拋物線平移，設(shè)平移后的拋物線為y=-x2+px+q,過點A與點（1，2），且m-q=25，在平移過程中，若拋物線y=-x2+bx+c向下平移了S（S＞0）個單位長度，求S的取值范圍．
【考點】二次函數(shù)圖象與幾何變換．
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：2403引用：7難度：0.4
相似題
-
1．將拋物線y=x2先向右平移5個單位長度，再向上平移3個單位長度，所得到的拋物線的解析式為（ ）
發(fā)布：2025/6/7 19:0:2組卷：526引用：11難度：0.6 -
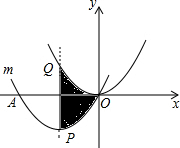2．如圖，把拋物線y=x2平移得到拋物線m,拋物線m經(jīng)過點A（-6，0）和原點O（0，0），它的頂點為P，它的對稱軸與拋物線y=12x2交于點Q，則圖中陰影部分的面積為（ ）12發(fā)布：2025/6/8 8:0:6組卷：460引用：2難度：0.9 -
3．在平面直角坐標(biāo)系中，點P的坐標(biāo)為（1，2），將拋物線y=
x2-3x+2沿坐標(biāo)軸平移一次，使其經(jīng)過點P，則平移的最短距離為（ ）12發(fā)布：2025/6/8 2:0:5組卷：1235引用：5難度：0.6