如圖，要修建一個圓形噴水池，在池中心O點(diǎn)豎直安裝一根水管，在水管的頂端A處安一個噴水頭，使噴出的拋物線形水柱在與池中心O點(diǎn)的水平距離為1m處達(dá)到最高，高度為3m,水柱落地處離池中心O點(diǎn)3m.則水管OA的高是?（ ）
【考點(diǎn)】二次函數(shù)的應(yīng)用．
【答案】B
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/14 10:0:8組卷：198引用：4難度：0.5
相似題
-
1．孔子曰：溫故而知新，可以為師矣．根據(jù)艾賓浩斯遺忘曲線，小蘇同學(xué)發(fā)現(xiàn)對所學(xué)知識點(diǎn)進(jìn)行復(fù)習(xí)回顧，學(xué)習(xí)效果會更好．某一天他利用30分鐘時間進(jìn)行自主學(xué)習(xí)．假設(shè)他用于學(xué)習(xí)的時間x（單位：分鐘）與學(xué)習(xí)收益量y的關(guān)系如圖甲所示，用于復(fù)習(xí)的時間x（單位：分鐘）與學(xué)習(xí)收益量y的關(guān)系如圖乙所示（其中OA是拋物線的一部分，A為拋物線的頂點(diǎn)）．
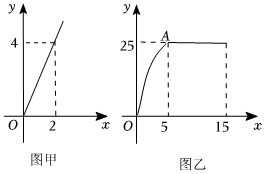
（1）求該同學(xué)的學(xué)習(xí)收益量y與用于學(xué)習(xí)的時間x之間的函數(shù)關(guān)系式，并直接寫出自變量x的取值范圍；
（2）求該同學(xué)的學(xué)習(xí)收益量y與用于復(fù)習(xí)的時間x之間的函數(shù)關(guān)系式；
（3）該同學(xué)應(yīng)如何分配學(xué)習(xí)和復(fù)習(xí)的時間，才能使這30分鐘的學(xué)習(xí)收益總量最大？（學(xué)習(xí)收益總量=解題的學(xué)習(xí)收益量+回顧反思的學(xué)習(xí)收益量）發(fā)布：2025/5/24 20:0:2組卷：170引用：2難度：0.3 -
2．巴中市某中學(xué)為增強(qiáng)學(xué)生運(yùn)用數(shù)學(xué)知識解決實(shí)際問題的能力，該校九（1）班同學(xué)進(jìn)行了一次市場調(diào)查，收集整理了一種進(jìn)價每件20元的商品在第x（1≤x≤70）天售價與銷量的相關(guān)信息，得到如下統(tǒng)計(jì)表．
（1）求這種商品每天銷售利潤y（元）與時間x的函數(shù)解析式；時間x（天） 1≤x＜40 40≤x≤70 售價（元/件） x+30 50 每天銷量（件） 160-2x
（2）銷售第幾天，當(dāng)天銷售利潤最大，并求出最大利潤；
（3）在銷售過程中，每天銷售利潤大于2250元共有多少天？發(fā)布：2025/5/24 20:0:2組卷：104引用：2難度：0.4 -
3．某商場將進(jìn)價為2000元的冰箱以2400元售出，平均每天能售出8臺，為了配合國家“家電下鄉(xiāng)”政策的實(shí)施，商場決定采取適當(dāng)?shù)慕祪r措施．調(diào)查表明：這種冰箱的售價每降低50元，平均每天就能多售出4臺．
（1）假設(shè)每臺冰箱降價x元，商場每天銷售這種冰箱的利潤是y元，請寫出y與x之間的函數(shù)表達(dá)式；（不要求寫自變量的取值范圍）
（2）商場要想在這種冰箱銷售中每天盈利4800元，同時又要使百姓得到實(shí)惠，每臺冰箱應(yīng)降價多少元？
（3）每臺冰箱降價多少元時，商場每天銷售這種冰箱的利潤最高？最高利潤是多少？發(fā)布：2025/5/24 20:0:2組卷：2657引用：119難度：0.1