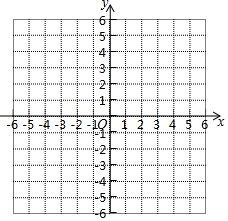
對(duì)于平面內(nèi)任意一個(gè)角的“夾線圓”，給出如下定義：如果一個(gè)圓與這個(gè)角的兩邊都相切，則稱這個(gè)圓為這個(gè)角的“夾線圓”．例如：在平面直角坐標(biāo)系xOy中，以點(diǎn)（1，1）為圓心，1為半徑的圓是x軸與y軸所構(gòu)成的直角的“夾線圓”．
（1）下列各點(diǎn)A（2，2），B（3，1），C（-1，0），D（1，-1）中，可以作為x軸與y軸所構(gòu)成的直角的“夾線圓”的圓心的點(diǎn)是A，DA，D；
（2）若⊙P為y軸和直線l：y=33x所構(gòu)成的銳角的“夾線圓”，且⊙P的半徑為1，求點(diǎn)P的坐標(biāo)．
（3）若⊙Q為x軸和直線??=-3??+23所構(gòu)成的銳角的“夾線圓”，且⊙Q的半徑1≤r≤2，直接寫(xiě)出點(diǎn)Q橫坐標(biāo)xQ的取值范圍．
3
3
3
3
【考點(diǎn)】一次函數(shù)綜合題．
【答案】A，D
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：128引用：1難度：0.3
相似題
-
1．如圖1，直線y=-
x+6與y軸交于點(diǎn)A，與x軸交于點(diǎn)D，直線AB交x軸于點(diǎn)B，△AOB沿直線AB折疊，點(diǎn)O恰好落在直線AD上的點(diǎn)C處．34
（1）求直線AB的解析式；
（2）如圖2，過(guò)點(diǎn)D作DE⊥AB于E，F(xiàn)是第四象限直線AB上一點(diǎn)，當(dāng)△DFE是等腰直角三角形時(shí)，求點(diǎn)F的坐標(biāo)；
（3）如圖3，點(diǎn)P是直線AB上一點(diǎn)，點(diǎn)Q是直線AD上一點(diǎn)，且P，Q均在第四象限，點(diǎn)E是x軸上一點(diǎn)，若四邊形PQDE為菱形，求點(diǎn)E的坐標(biāo)．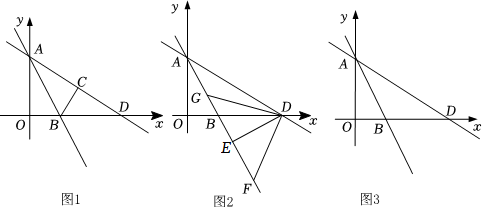
發(fā)布：2025/6/13 1:30:1組卷：346引用：1難度：0.3 -
2．在平面直角坐標(biāo)系中，直線l1：y=2x+3與過(guò)點(diǎn)B（6，0）的直線l2交于點(diǎn)C（1，m），與x軸交于點(diǎn)A，與y軸交于點(diǎn)E，直線l2與y軸交于點(diǎn)D．
（1）求直線l2的函數(shù)解析式；
（2）如圖1，點(diǎn)F在直線l2位于第二象限的圖象上，使得S△BEF=4?S△OEF，求點(diǎn)F的坐標(biāo)．
（3）如圖2，在線段BC存在點(diǎn)M，使得△CEM是以CM為腰的等腰三角形，求M點(diǎn)坐標(biāo)．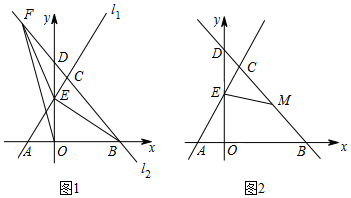
發(fā)布：2025/6/12 12:30:1組卷：1658引用：3難度：0.4 -
3．在平面直角坐標(biāo)系xOy中，對(duì)于點(diǎn)A，記線段OA的中點(diǎn)為M．若點(diǎn)A，M，P，Q按逆時(shí)針?lè)较蚺帕袠?gòu)成菱形AMPQ，其中∠QAM=α（0°＜α＜180°），則稱菱形AMPQ是點(diǎn)A的“α-旋半菱形”，稱菱形AMPQ邊上所有點(diǎn)都是點(diǎn)A的“α-旋半點(diǎn)”．已知點(diǎn)A（-4，0）．
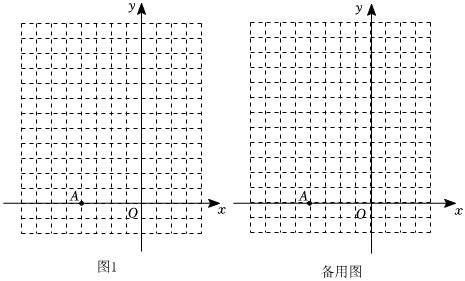
（1）在圖1中，畫(huà)出點(diǎn)A的“30°-旋半菱形”AMPQ，并直接寫(xiě)出點(diǎn)P的坐標(biāo)；
（2）若點(diǎn)B（-1，1）是點(diǎn)A的“α-旋半點(diǎn)”，求α的值；
（3）若存在α使得直線上有點(diǎn)A的“α-旋半點(diǎn)”，直接寫(xiě)出b的取值范圍．y=3x+b發(fā)布：2025/6/12 22:30:1組卷：185引用：1難度：0.1