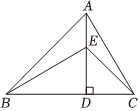
AD⊥BC，垂足為點D，AD=BD，點E在AD上，∠CED=45°，請寫出圖中相等的線段；并給出證明（不包括已知條件中的相等線段）．
【考點】全等三角形的判定與性質(zhì)．
【答案】DE=DC，BE=AC，證明見解析．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/12 13:0:9組卷：3引用：2難度：0.5
相似題
-
1．如圖1，在△ABC中，AB=AC，點D，E在BC上，且BD=CE，連接AD，AE．
（1）判斷AD與AE的數(shù)量關(guān)系，并說明理由；
（2）如圖2，過點B作BF∥AC，交AD的延長線于點F．若∠DAE=∠C=α，請直接寫出圖2中所有頂角為α的等腰三角形．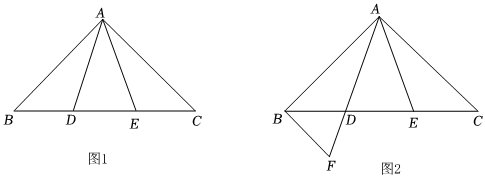
?發(fā)布：2025/5/23 19:30:1組卷：308引用：3難度：0.6 -
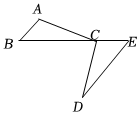2．如圖，C為BE上一點AB∥DE，AB=CE，BC=DE．求證：AC=CD．發(fā)布：2025/5/23 19:30:1組卷：129引用：1難度：0.6 -
3．綜合與實踐
小明遇到這樣一個問題，如圖1，△ABC中，AB=7，AC=5，點D為BC的中點，求AD的取值范圍．
小明發(fā)現(xiàn)老師講過的“倍長中線法”可以解決這個問題，所謂倍長中線法，就是將三角形的中線延長一倍，以便構(gòu)造出全等三角形，從而運用全等三角形的有關(guān)知識來解決問題的方法，他的做法是：如圖2，延長AD到E，使DE=AD，連接BE，構(gòu)造△BED≌△CAD，經(jīng)過推理和計算使問題得到解決．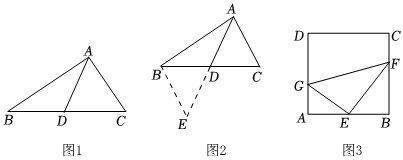
請回答：
（1）小明證明△BED≌△CAD用到的判定定理是：；（填入你選擇的選項字母）
A．SAS
B．SSS
C．AAS
D．ASA
（2）AD的取值范圍是 ．
小明還發(fā)現(xiàn)：倍長中線法最重要的一點就是延長中線一倍，完成全等三角形模型的構(gòu)造．
參考小明思考問題的方法，解決問題：
如圖3，在正方形ABCD中，E為AB邊的中點，G、F分別為AD，BC邊上的點，若AG=2，BF=4，∠GEF=90°，求GF的長．發(fā)布：2025/5/23 19:30:1組卷：815引用：3難度：0.5