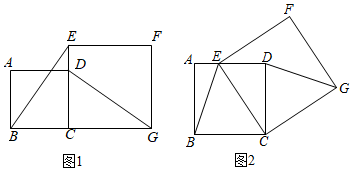
問題情境：（1）如圖1，已知正方形ABCD，點E在CD的延長線上，以CE為邊構造正方形CEFG，連接BE和DG，則BE和DG的關系為 BE=DG，BE⊥DGBE=DG，BE⊥DG．
繼續探究：（2）如圖2所示，已知正方形ABCD，點E是線段AD上的一點，以CE為邊在CE的右側作正方形CEFG，連接DG、BE．問（1）中結論是否仍然成立？若成立，請證明；若不成立，請說明理由．
拓展應用：（3）若正方形ABCD的邊長為3，點E是直線AD上的一個動點，以CE為邊在CE的右側作正方形CEFG，連接DG、BE、BG，若AE=1，畫出圖形，并直接寫出BG長．
【考點】四邊形綜合題．
【答案】BE=DG，BE⊥DG
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：118引用：1難度：0.3
相似題
-
1．已知正方形ABCD，點F是射線DC上一劫點（不與C、D重合）．連接AP并延長交直線BC于點E，交BD于H，連接CH，過點C作CG⊥HC交AE于點G．
（1）若點F在邊CD上，如圖1，
①證明：∠DAF=∠DCF；
②猜想△GFC的形狀并說明理由．
（2）取DF中點M，連接MG．若MG=2.5，正方形邊長為4，求BE的長．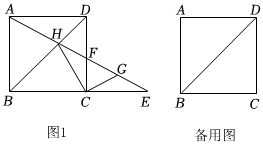
發布：2025/6/11 3:30:1組卷：18引用：1難度：0.2 -
2．（1）方法回顧
證明：三角形中位線定理．
已知：如圖1，DE是△ABC的中位線．
求證：．
證明：（請在答題紙上完成證明過程）
（2）問題解決
如圖2，在正方形ABCD中，E為AD的中點，G、F分別為AB、CD邊上的點，若AG=3，DF=4，∠GEF=90°，求GF的長．
（3）拓展研究
如圖3，在四邊形ABCD中，∠A=105°，∠D=120°，E為AD的中點，G、F分別為AB、CD邊上的點，若AG=2，，∠GEF=90°，求GF的長．DF=2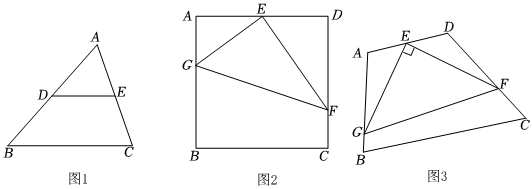
發布：2025/6/11 3:30:1組卷：167引用：1難度：0.2 -
3．（1）【定義理解】如圖1，在△ABC中，E是BC的中點，P是AE的中點，就稱CP是△ABC的“雙中線”，∠ACB=90°，AC=3，AB=5，則CP=．
（2）【類比探究】
①如圖2，E是菱形ABCD一邊上的中點，P是BE上的中點，則稱AP是菱形ABCD的“雙中線”，若AB=4，∠BAD=120°，則AP=．
②如圖3，AP是矩形ABCD的“雙中線”，若AB=4，BC=6，求AP的長．
（3）【拓展應用】
如圖4，AP是平行四邊形ABCD的“雙中線”，若AB=4，BC=6，∠BAD=120°，求AP的長．發布：2025/6/11 2:30:2組卷：704引用：4難度：0.4