【閱讀材料】利用公式法，可以將一些形如ax2+bx+c（a≠0）的多項式變形為a（x+m）2+n的形式，我們把這樣的變形方法叫做多項式ax2+bx+c（a≠0）的配方法，運用多項式的配方法及平方差公式能對一些多項式進行因式分解或有關運算．
例如：對于a2+6a+8．（1）用配方法分解因式；（2）當a取何值，代數式a2+6a+8有最小值？最小值是多少？
解：（1）原式=a2+6a+8+1-1=a2+6a+9-1=（a+3）2-1=[（a+3）+1][（a+3）-1]=（a+4）（a+2）．
（2）由（1）得：a2+6a+8=（a+3）2-1∵（a+3）2≥0，∴（a+3）2-1≥-1，∴當a=-3時，代數式a2+6a+8有最小值，最小值是-1．
【問題解決】利用配方法解決下列問題：
（1）用配方法因式分解：x2+2x-8；
（2）試說明不論m為何值，代數式-m2+4m-5恒為負數；
（3）若已知（a+c）（b-a）=14（b+c）2且a≠0，求b-ca的值．
1
4
（
b
+
c
）
2
b
-
c
a
【答案】（1）x2+2x-8=（x+4）（x-2）；
（2）見解答；
（3）2．
（2）見解答；
（3）2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：186引用：1難度：0.4
相似題
-
1．【知識再現】在研究平方差公式時，我們在邊長為a的正方形中剪掉一個邊長為b的小正方形（如圖1），把余下的陰影部分再剪拼成一個長方形（如圖2），根據圖1、圖2陰影部分的面積關系，可以得到一個關于a,b的等式①；
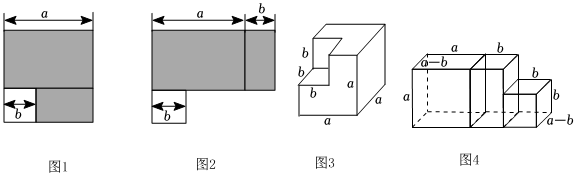
【知識遷移】在棱長為a的正方體上挖去一個棱長為b的小正方體后，余下的部分（如圖3）再切割拼成一個幾何體（如圖4）．根據它們的體積關系得到關于a,b的等式為②a3-b3=（結果寫成整式的積的形式）
【知識運用】已知a-b=4，ab=3，求a3-b3的值．發布：2025/6/5 7:0:2組卷：1069引用：8難度：0.5 -
2．我們知道，對于一個圖形，通過兩種不同的方法計算它的面積，可以得到一個數學等式．例如圖1可以得到（a+2b）（a+b）=a2+3ab+2b2，請解答下列問題：如圖2，已知a+b+c=12，ab+bc+ac=38，則a2+b2+c2=．發布：2025/6/5 6:0:2組卷：222引用：2難度：0.6 -
3．若一個四位數M的千位數字與個位數字之差為2，百位數字與十位數字之和為8，則這個四位數M為“二八數”；若四位數M的千位數字和百位數字交換順序，十位數字和個位數字交換順序得到一個新的四位數字N，此時稱N是M的“友好數”，并規定
．例如：M=7265，因為7-5=2，2+6=8，所以7265是“二八數”，則它的“友好數”N=2756．F（M）=M-N9
（1）請判斷3531，4713是否是“二八數”，并說明理由；如果是，請計算F（M）；
（2）一個“二八數”M的千位數字為a,百位數字為b,十位數字為c,個位數字為d,記，D（M）=a+b10，當D（M），E（M）均是整數時，求出所有滿足條件的M．E（M）=F（M）3發布：2025/6/5 5:30:2組卷：213引用：3難度：0.5