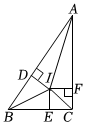
如圖，將直角三角形分割成一個正方形和兩對全等的直角三角形，直角三角形ABC中，∠ACB=90°，BC=a,AC=b,AB=c,正方形IECF中，IE=EC=CF=FI=x,小明發現了求正方形邊長的方法：
由題意可得BD=BE=a-x,AD=AF=b-x,
因為AB=BD+AD，所以a-x+b-x=c,解得x=a+b-c2．
（1）小亮也發現了另一種求正方形邊長的方法：利用S△ABC=S△AIB+S△BIC+S△AIC，可以得到x與a、b、c的關系，請根據小亮的思路完成他的求解過程．
（2）請結合小明和小亮得到的結論驗證勾股定理．
x
=
a
+
b
-
c
2
【考點】勾股定理的證明．
【答案】（1）見解析部分；
（2）證明見解析部分．
（2）證明見解析部分．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：90引用：1難度：0.5
相似題
-
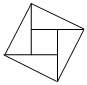1．如圖是一個“趙爽弦圖”，它是由四個全等的直角三角形圍成一個大正方形，中空的部分也是一個小正方形，若大正方形的邊長為7，小正方形的邊長為3，直角三角形的兩直角邊分別為a,b,則ab的值為 ．發布：2025/6/7 11:0:1組卷：255引用：5難度：0.7 -
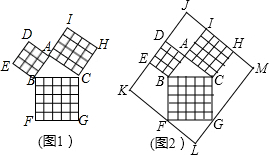2．勾股定理在平面幾何中有著不可替代的重要地位，在我國古算書《周髀算經》中就有“若勾三，股四，則弦五”的記載．如圖1是由邊長均為1的小正方形和Rt△ABC構成的，可以用其面積關系驗證勾股定理．將圖1按圖2所示“嵌入”長方形LMJK，則該長方形的面積為（ ）發布：2025/6/8 3:0:2組卷：1952引用：7難度：0.5 -
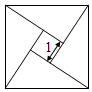3．如圖，“趙爽弦圖”是由四個全等的直角三角形與一個小正方形拼成大正方形，若小正方形邊長為1，大正方形邊長為5，則一個直角三角形的周長是（ ）發布：2025/6/8 2:0:5組卷：1587引用：5難度：0.5