已知雙曲線x2a2-y2b2=1，（a＞0，b＞0）的離心率為2，右焦點F到漸近線的距離為3．
（1）求雙曲線的標準方程；
（2）若點P為雙曲線右支上一動點，過點P與雙曲線相切的直線l,直線l與雙曲線的漸近線分別交于M，N兩點，求△FMN的面積的最小值．
x
2
a
2
-
y
2
b
2
=
1
，
（
a
＞
0
，
b
＞
0
）
3
【考點】雙曲線的切線方程及性質．
【答案】1）；
（2）．
x
2
-
y
2
3
=
1
（2）
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/20 7:0:8組卷：136引用：2難度：0.5
相似題
-
1．已知雙曲線C：
=1（a＞0，b＞0）上任意一點P（異于頂點）與雙曲線兩頂點連線的斜率之積為x2a2-y2b2，E在雙曲線C上，F為雙曲線C的右焦點，|EF|的最小值為2-13．3
（1）求雙曲線C的標準方程；
（2）設O為坐標原點，直線l為雙曲線C的切線，過F作l的垂線，垂足為A，求證：A在定圓上．發布：2024/6/27 10:35:59組卷：71引用：1難度：0.3 -
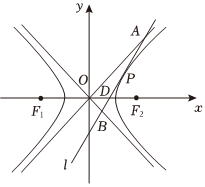2．如圖，O為坐標原點，F1，F2分別為雙曲線的左、右焦點，過雙曲線C右支上一點P作雙曲線的切線l分別交兩漸近線于A、B兩點，交x軸于點D，則下列結論正確的是（ ）C：x2-y2b2=1（b＞0）發布：2024/4/26 11:36:51組卷：229引用：3難度：0.2 -
3．已知F1，F2分別為雙曲線C：
的左、右焦點，點A（x1，y1）為雙曲線C在第一象限的右支上一點，以A為切點作雙曲線C的切線交x軸于點B，若x2a2-y2b2=1（a＞0，b＞0），且cos∠F1AF2=12，則雙曲線C的離心率為（ ）F1B=2BF2發布：2024/10/22 8:0:1組卷：69引用：2難度：0.5