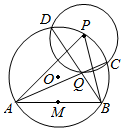
如圖，已知AB為⊙O的弦，M為AB的中點，P為⊙O上任意一點，以點P為圓心、2MO為半徑作圓并交⊙O于點C、D，AC、BD交于點Q，請問：
（1）點Q是△PAB的什么“心”？
（2）點Q是否在⊙P上？試證明你的結論．
提示：（1）三角形的三條高線交于一點，稱為垂心定理，此點稱為垂心．
（2）三角形有內心、外心、重心、垂心等．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：23引用：1難度：0.5
相似題
-
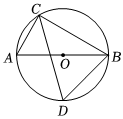1．如圖，⊙O的直徑AB為10cm,弦AC為5cm,∠ACB的角平分線交圓于點D，則∠CBD的度數為（ ）發布：2025/5/22 5:30:2組卷：119引用：3難度：0.6 -
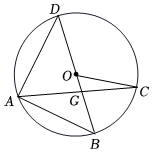2．如圖，BD是圓O的直徑，點A，C在圓上，若∠COD=126°，則∠BAC=（ ）發布：2025/5/22 4:0:7組卷：48引用：2難度：0.7 -
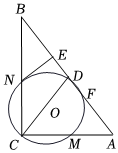3．如圖，在Rt△ABC中，∠ACB=90°，CD是斜邊AB上的中線，以CD為直徑的⊙O分別交AC、BC于點M、N，交AB于點D、F（D、F可重合），過點N作NE⊥AB，垂足為E．
（1）求證：BN=CN；
（2）填空：
①當∠DCA的度數為 時，四邊形DENO為正方形；
②當∠DCA的度數為 時，四邊形AFOM為菱形．發布：2025/5/22 6:0:1組卷：225引用：3難度：0.5
相關試卷