2006年山西省太原市初中數學競賽試卷

一、選擇題（共6小題，每小題7分，滿分42分）

• 1．若x+y=1，x³+y³=

  1

  3

  ，則x⁵+y⁵的值是（　　）

  A． 11 81

  B． 31 81

  C． 11 243

  D． 31 243
  組卷：1312引用：2難度：0.9

  解析

• 2．已知2x-3

  xy

  -2y=0（x＞0），則

  x

  2

  +

  4

  xy

  -

  16

  y

  2

  2

  x

  2

  +

  xy

  -

  9

  y

  2

  的值是（　　）

  A． 2 3

  B． 4 9

  C． 16 25

  D． 16 27
  組卷：283引用：2難度：0.9

  解析

• 3．在凸多邊形中，四邊形有兩條對角線，五邊形有5條對角線．觀察探索凸十邊形有（　　）條對角線．

  A．29

  B．32

  C．35

  D．38
  組卷：325引用：3難度：0.9

  解析

• 4．已知△ABC中，AB=AC=8

  3

  ，高AD=8，則△ABC外接圓的半徑為（　　）

  A．8

  B．9

  C．10

  D．12
  組卷：112引用：3難度：0.9

  解析

• 5．若一個正整數能表示為兩個正整數的平方差，則稱這個正整數為“智慧數”（如3=2²-1²，16=5²-3²）．已知智慧數按從小到大順序構成如下數列：
  3，5，7，8，9，11，12，13，15，16，17，19，20，21，23，24，25，…．
  則第2006個智慧數是（　　）

  A．2672

  B．2675

  C．2677

  D．2680
  組卷：495引用：6難度：0.9

  解析

三、解答題（共4小題，滿分66分）

• 15．求方程2x²+5xy+2y²=2006的所有正整數解．
  組卷：198引用：1難度：0.1

  解析

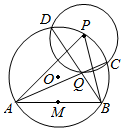• 16．如圖，已知AB為⊙O的弦，M為AB的中點，P為⊙O上任意一點，以點P為圓心、2MO為半徑作圓并交⊙O于點C、D，AC、BD交于點Q，請問：
  （1）點Q是△PAB的什么“心”？
  （2）點Q是否在⊙P上？試證明你的結論．
  提示：（1）三角形的三條高線交于一點，稱為垂心定理，此點稱為垂心．
  （2）三角形有內心、外心、重心、垂心等．
  組卷：23引用：1難度：0.5

  解析