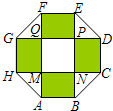
某住宅小區(qū)，為美化環(huán)境，提高居民區(qū)生活質(zhì)量，要建一個(gè)八邊形居民廣場(chǎng)（平面圖如圖所示），其中，正方形MNPQ與四個(gè)相同矩形（圖中陰影部分）的面積的和為800平方米．
（1）設(shè)矩形的邊長(zhǎng)AB=x（米），AM=y（米），用含x的代數(shù)式表示y；
（2）現(xiàn)計(jì)劃在正方形區(qū)域上建雕塑和花壇，平均每平方米造價(jià)為2100元，在四個(gè)相同的矩形區(qū)域上鋪設(shè)花崗巖地坪，平均每平方米造價(jià)為105元，在四個(gè)三角形區(qū)域上鋪設(shè)草坪，平均每平方米造價(jià)為40元．
①設(shè)該工程的總造價(jià)為S（元），求S關(guān)于x的函數(shù)關(guān)系式；
②若該工程的銀行貸款為235000元，問(wèn)僅靠銀行貸款能否完成該工程的建設(shè)任務(wù)？若能，請(qǐng)列出設(shè)計(jì)方案；若不能請(qǐng)說(shuō)明理由；
③若該工程在銀行貸款的基礎(chǔ)上，又增加獎(jiǎng)金73000元，問(wèn)能否完成該工程的建設(shè)任務(wù)？若能，請(qǐng)列出所有可能的設(shè)計(jì)方案；若不能，請(qǐng)說(shuō)明理由．
【考點(diǎn)】二次函數(shù)的應(yīng)用．
【答案】見(jiàn)試題解答內(nèi)容
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：148引用：4難度：0.1
相似題
-
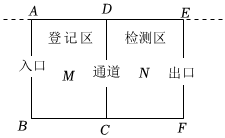1．為了有效預(yù)防和控制疫情，及時(shí)監(jiān)測(cè)疫情發(fā)展態(tài)勢(shì)，實(shí)施定期核酸檢測(cè)．某社區(qū)準(zhǔn)備搭建一個(gè)動(dòng)態(tài)核酸檢測(cè)點(diǎn)，現(xiàn)有33米可移動(dòng)的隔離帶，圍成如圖的臨時(shí)檢測(cè)點(diǎn)，這是一個(gè)一面靠墻（墻面為AE）的矩形，內(nèi)部分成兩個(gè)區(qū)，M區(qū)為登記區(qū)，N區(qū)為檢測(cè)區(qū)，入口通道在AB邊上，兩區(qū)通道在CD邊上，出口通道在EF邊上，通道寬均為1米．設(shè)AB=x,矩形ABFE的面積為w.
（1）BF可表示為 ；
（2）當(dāng)x為何值時(shí)，w有最大值？最大值是多少？
（3）所圍成矩形ABFE的面積能否達(dá)到96平方米？如果能，求出AB的長(zhǎng)；如果不能，請(qǐng)說(shuō)明理由．發(fā)布：2025/6/1 0:30:1組卷：99引用：2難度：0.6 -
2．某企業(yè)銷售一種日用產(chǎn)品，該產(chǎn)品每件的成本是20元．經(jīng)市場(chǎng)調(diào)查表明，當(dāng)每件產(chǎn)品售價(jià)在24～35元之間（含24，35）浮動(dòng)時(shí)，售價(jià)每增加1元，日均銷售量減少40件；當(dāng)每件產(chǎn)品售價(jià)為25元時(shí)，日均銷售量為600件．設(shè)每件產(chǎn)品的售價(jià)為x元（x為整數(shù)且24≤x≤35），日均銷售量為y件．
（1）求y關(guān)于x的函數(shù)表達(dá)式．
（2）設(shè)銷售該產(chǎn)品日均利潤(rùn)為W元，當(dāng)售價(jià)為多少元時(shí)，日均利潤(rùn)獲得最大？最大值是多少？
（3）為促進(jìn)公益，該企業(yè)決定，在保證該企業(yè)日均利潤(rùn)不低于3800元的情況下，將超出部分的m元全部捐贈(zèng)給慈善機(jī)構(gòu)，求日均捐贈(zèng)數(shù)額m的所有可能值．發(fā)布：2025/6/1 1:0:1組卷：85引用：1難度：0.4 -
3．某批發(fā)市場(chǎng)批發(fā)甲、乙兩種水果，根據(jù)以往經(jīng)驗(yàn)和市場(chǎng)行情，預(yù)計(jì)夏季某一段時(shí)間內(nèi)，甲種水果的銷售利潤(rùn)y甲（萬(wàn)元）與進(jìn)貨量x（噸）近似滿足函數(shù)關(guān)系y甲=0.3x；乙種水果的銷售利潤(rùn)y乙（萬(wàn)元）與進(jìn)貨量x（噸）近似滿足函數(shù)關(guān)系y乙=ax2+bx（其中a≠0，a,b為常數(shù)），且進(jìn)貨量x為1噸時(shí)，銷售利潤(rùn)y乙為1.4萬(wàn)元；進(jìn)貨量x為2噸時(shí)，銷售利潤(rùn)y乙為2.6萬(wàn)元．
（1）求y乙（萬(wàn)元）與x（噸）之間的函數(shù)關(guān)系式．
（2）如果市場(chǎng)準(zhǔn)備進(jìn)甲、乙兩種水果共10噸，設(shè)乙種水果的進(jìn)貨量為t噸，請(qǐng)你寫出這兩種水果所獲得的銷售利潤(rùn)之和W（萬(wàn)元）與t（噸）之間的函數(shù)關(guān)系式．并求出這兩種水果各進(jìn)多少噸時(shí)獲得的銷售利潤(rùn)之和最大，最大利潤(rùn)是多少？發(fā)布：2025/6/1 1:0:1組卷：303引用：23難度：0.1