2010年新課標九年級數學競賽培訓第24講：幾何的定值與最值

一、填空題（共4小題，每小題5分，滿分20分）

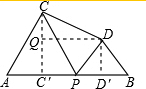• 1．如圖，已知AB=10，P是線段AB上任意一點，在AB的同側分別以AP和PB為邊作等邊△APC和等邊△BPD，則CD長度的最小值為

   

  ．
  組卷：358引用：3難度：0.7

  解析

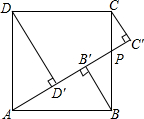• 2．如圖，正方形ABCD的邊長為1，點P為邊BC上任意一點（可與B點或C點重合），分別過B、C、D作射線AP的垂線，垂足分別是B′、C′、D′，則BB′+CC′+DD′的最大值為

  ，最小值為

  ．
  組卷：2507引用：10難度：0.5

  解析

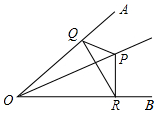• 3．如圖，∠AOB=45°，角內有點P，PO=10，在角的兩邊上有兩點Q，R（均不同于O點），則△PQR的周長的最小值為

  ．
  組卷：428引用：7難度：0.5

  解析

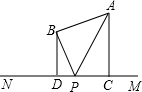• 4．如圖，兩點A、B在直線MN外的同側，A到MN的距離AC=8，B到MN的距離BD=5，CD=4，P在直線MN上運動，則|PA-PB|的最大值等于

   

  ．
  組卷：1302引用：10難度：0.7

  解析

二、選擇題（共6小題，每小題4分，滿分24分）

• 5．如圖，圓的半徑等于正三角形ABC的高，此圓在沿底邊AB滾動，切點為T，圓交AC、BC于M、N，則對于所有可能的圓的位置而言，

  ?

  MTN

  的度數為（　　）

  A．從30°到60°變動	B．從60°到90°變動
  C．保持30°不變	D．保持60°不變
  組卷：280引用：3難度：0.6

  解析

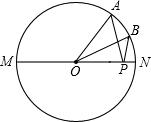• 6．如圖，A點是半圓上一個三等分點，B點是弧AN的中點，P點是直徑MN上一動點，⊙O的半徑為1，則AP+BP的最小值為（　　）

  A．1

  B． 2 2

  C． 2

  D． 3 - 1
  組卷：960引用：15難度：0.7

  解析

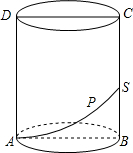• 7．如圖，圓柱的軸截面ABCD是邊長為4的正方形，動點P從A點出發，沿著圓柱的側面移動到BC的中點S的最短距離為（　　）

  A． 2 1 + π 2

  B． 2 1 + 4 π 2

  C． 4 1 + π 2

  D． 2 4 + π 2
  組卷：1002引用：13難度：0.5

  解析

三、解答題（共11小題，滿分106分）

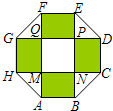• 20．某住宅小區，為美化環境，提高居民區生活質量，要建一個八邊形居民廣場（平面圖如圖所示），其中，正方形MNPQ與四個相同矩形（圖中陰影部分）的面積的和為800平方米．
  （1）設矩形的邊長AB=x（米），AM=y（米），用含x的代數式表示y；
  （2）現計劃在正方形區域上建雕塑和花壇，平均每平方米造價為2100元，在四個相同的矩形區域上鋪設花崗巖地坪，平均每平方米造價為105元，在四個三角形區域上鋪設草坪，平均每平方米造價為40元．
  ①設該工程的總造價為S（元），求S關于x的函數關系式；
  ②若該工程的銀行貸款為235000元，問僅靠銀行貸款能否完成該工程的建設任務？若能，請列出設計方案；若不能請說明理由；
  ③若該工程在銀行貸款的基礎上，又增加獎金73000元，問能否完成該工程的建設任務？若能，請列出所有可能的設計方案；若不能，請說明理由．
  組卷：148引用：4難度：0.1

  解析

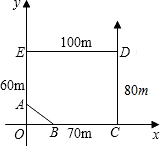• 21．某房地產公司擁有一塊“缺角矩形”荒地ABCDE，邊長和方向如圖，欲在這塊地上建一座地基為長方形東西走向的公寓，請劃出這塊地基，并求地基的最大面積（精確到1m²）．
  組卷：132引用：4難度：0.5

  解析