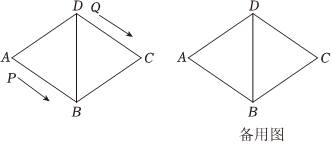
如圖，菱形ABCD的邊長為12cm,∠A=60°，動點P從點A出發，沿著線路AB-BD做勻速運動，動點Q從點D同時出發，沿著線路DC-CB-BA做勻速運動．
（1）求BD的長；
（2）已知動點P運動的速度為2cm/s,動點Q運動的速度為2.5cm/s.經過12秒后，P、Q分別到達M、N兩點，試判斷△AMN的形狀，并說明理由；
（3）設問題（2）中的動點P、Q分別從M、N同時沿原路返回，動點P的速度不變，動點Q的速度改變為a cm/s,經過2秒后，P、Q分別到達E、F兩點，若△BEF為直角三角形，試求a值．
【考點】四邊形綜合題．
【答案】（1）BD=12；
（2）△AMN為直角三角形，理由見解答過程；
（3）若△BEF為直角三角形，a的值為1或5或7．
（2）△AMN為直角三角形，理由見解答過程；
（3）若△BEF為直角三角形，a的值為1或5或7．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/8 8:0:9組卷：61引用：1難度：0.1
相似題
-
1．如圖①，△ABC是等腰直角三角形，
∠BAC=90°，AB=AC，四邊形ADEF是正方形，點B、C分別在邊AD、AF上，此時BD=CF，BD⊥CF成立．
將△ABC繞點A逆時針旋轉α（0°＜α＜90°），并探究下列問題：
（1）如圖②，BD=CF成立嗎？若成立，請證明；若不成立，請說明理由；
（2）當α=45°時，如圖③，延長DB交CF于點H．當AB=2，AD=3時，求線段DH的長；2
（3）如圖④，延長DB交CF于點H，連接AH，直接寫出線段FH，DH，AH之間的數量關系．發布：2025/6/6 7:0:2組卷：276引用：1難度：0.1 -
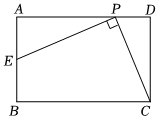2．如圖，在矩形ABCD中，AB=6，BC=9，P是線段AD邊上的任意一點（不含端點A、D），連接PC，過點P作PE⊥PC交AB于E．
（1）若DP=2，則AE=；
（2）當點P在AD上運動時，對應的點E也隨之在AB上運動，求BE的取值范圍；
（3）在線段AD上是否存在不同于P的點Q，使得QC⊥QE？若存在，求線段AP與AQ之間的數量關系；若不存在，請說明理由．發布：2025/6/6 7:0:2組卷：92引用：1難度：0.1 -
3．折紙不僅是一項有趣的活動，也是一項益智的數學活動．今天，就讓我們帶著數學的眼光來玩一玩折紙，看著折疊矩形的對角線之后能得到哪些數學結論．
【實踐操作】將矩形紙片ABCD沿對角線AC翻折，使點D落矩形ABCD所在平面內，邊BC和AD'相交于點E．
【解決問題】
（1）如圖1，①求證：△ABE≌△CD'E；②連接BD'，判斷BD'和AC的位置，并說明理由；
（2）如圖2，在矩形ABCD中，若AB=3，點F是對角線AC上一動點，∠ACB=30°，連結EF，作點C關于直線EF的對稱點P，直線PE交AC于點Q，當△AEQ是直角三角形時，直接寫出CF的長．3
發布：2025/6/6 7:0:2組卷：272引用：4難度：0.3