閱讀下列材料，并完成相應(yīng)的任務(wù)：有趣的“飛鏢圖”．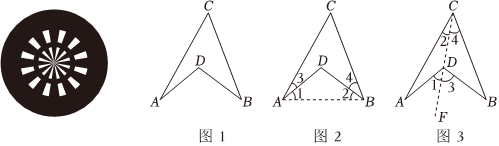
如圖1的四邊形ACBD，這種形似飛鏢的四邊形，我們形象地稱(chēng)它為“飛鏢圖”．它實(shí)際上就是凹四邊形，同學(xué)們通過(guò)探究發(fā)現(xiàn)：凹四邊形中最大內(nèi)角外面的角等于其余三個(gè)內(nèi)角之和，即如圖1，∠ADB=∠A+∠B+∠C．
“智慧小組”通過(guò)互學(xué)證明了這個(gè)結(jié)論：
方法一：如圖2，連結(jié)AB，則在△ABC中，∠C+∠CAB+∠CBA=180°，
即∠1+∠2+∠3+∠4+∠C=180°，
又∵在△ABD中，∠1+∠2+∠ADB=180°，
∴∠ADB=∠3+∠4+∠C，
即∠ADB=∠CAD+∠CBD+∠C．
“創(chuàng)新小組”想出了另外一種方法：
方法二：如圖3，連結(jié)CD并延長(zhǎng)至F，
∵∠1和∠3分別是△ACD和△BCD的一個(gè)外角，
…
任務(wù)：
（1）填空：“智慧小組”用的“方法一”主要依據(jù)的一個(gè)數(shù)學(xué)定理是 三角形內(nèi)角和定理三角形內(nèi)角和定理；
（2）根據(jù)“創(chuàng)新小組”“方法二”中輔助線(xiàn)的添加方式，寫(xiě)出該證明過(guò)程的剩余部分．
【考點(diǎn)】四邊形綜合題．
【答案】三角形內(nèi)角和定理
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/3 8:0:9組卷：66引用：3難度：0.1
相似題
-
1．（1）如圖1，在四邊形ABCD中，AB=AD，∠B=∠ADC=90°，點(diǎn)E、F分別在邊BC、CD上，且EF=BE+DF，探究圖中∠BAE、∠FAD、∠EAF之間的數(shù)量關(guān)系．
小明探究的方法是：延長(zhǎng)FD到點(diǎn)G，使DG=BE，連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結(jié)論，他的結(jié)論是 ．
（2）如圖2，在四邊形ABCD中，AB=AD，∠B+∠D=180°，點(diǎn)E、F分別在邊BC、CD上，且EF=BE+DF，探究上述結(jié)論是否仍然成立，并說(shuō)明理由．
（3）如圖3，在四邊形ABCD中，AB=AD，∠ABC+∠ADC=180°，若點(diǎn)E在CB的延長(zhǎng)線(xiàn)上，點(diǎn)F在CD的延長(zhǎng)線(xiàn)上，仍然滿(mǎn)足EF=BE+FD，請(qǐng)直接寫(xiě)出∠EAF與∠DAB的數(shù)量關(guān)系為 ．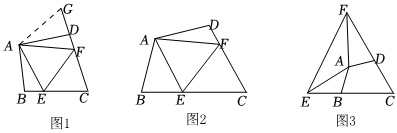
發(fā)布：2025/5/31 3:30:1組卷：181引用：2難度：0.1 -
2．如圖，在△ABC中，∠ABC=90°，∠ACB=30°，將△ABC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60°能與△DEC重合．
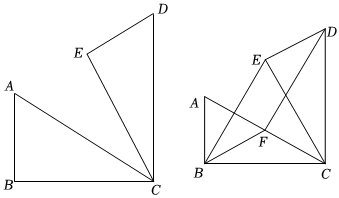
（1）請(qǐng)用尺規(guī)作圖法，作AC的垂直平分線(xiàn)，垂足為F；（不要求寫(xiě)作法，保留作圖痕跡）
（2）在（1）問(wèn)情況下，連接DF，求證：△CFD≌△ABC（填空）；
證明：（2）∵點(diǎn)F是邊AC中點(diǎn)，
∴CF=，
∵∠BCA=30°，∠ABC=90°
∴BA=AC，∠A=60°，12
∴AB=，
∵將△ABC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60°得到△DEC，
∴AC=CD，∠FCD=60°，
∴∠A=，
在△ABC和△CFD中，，①：AB=CF∠A=∠FCD（①）
∴△ABC≌△CFD（SAS）；
（3）在（1）問(wèn)情況下，連接BE，BF，DF，求證：四邊形BEDF是平行四邊形．發(fā)布：2025/5/31 5:30:3組卷：26引用：1難度：0.4 -
3．綜合與實(shí)踐圖形的幾何變換
復(fù)習(xí)課上，老師對(duì)一張平行四邊形紙片ABCD（AD＞AB）進(jìn)行如下操作：
（1）如圖1，折疊該紙片，使邊AB恰好落在邊AD上，邊CD恰好落在邊CB上，得到折痕AE和CF，判斷四邊形AECF的形狀并說(shuō)明理由；
（2）老師沿折痕將△ABE和△CDF剪下，得到兩個(gè)全等的等腰三角形，已知等腰三角形的腰長(zhǎng)為5，底邊長(zhǎng)為6，底角度數(shù)為α，通過(guò)不同的擺放方式，三個(gè)學(xué)習(xí)小組利用幾何變換設(shè)置了幾個(gè)問(wèn)題，請(qǐng)一一解答．
①善思小組：
將兩個(gè)三角形擺放成如圖2的位置，使邊CF與邊EA重合，然后固定△ABE，將△CDF沿著射線(xiàn)EA的方向平移，如圖3，當(dāng)四邊形FBED為矩形時(shí)，求平移的距離；
②勤學(xué)小組：
將兩個(gè)三角形擺成如圖4的位置，使△BAE與△DFC重合，取AE的中點(diǎn)O，固定△ABE，將△CDF繞著點(diǎn)O按逆時(shí)針?lè)较蛐D(zhuǎn)（0°＜旋轉(zhuǎn)角＜360°），如圖5，在旋轉(zhuǎn)過(guò)程中，四邊形ACEF的形狀是 ．
③奮進(jìn)小組：
在上面的旋轉(zhuǎn)過(guò)程中，利用圖6進(jìn)行探究，當(dāng)△BAE與△DFC的重疊部分為等腰三角形時(shí)，旋轉(zhuǎn)角為 （用含α的代數(shù)式表示），此時(shí)重疊部分的面積為 ．
發(fā)布：2025/5/30 23:30:1組卷：313引用：2難度：0.1