（1）若a,b為有理數(shù)，且2a2-2ab+b2+4a+4=0，a2b+ab2=-16-16；
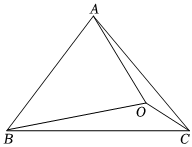
（2）如圖，在△ABC中，AB=AC，∠BAC=80°，O為△ABC內(nèi)一點(diǎn)，∠OBC=10°，∠OCB=30°，則∠BAO的度數(shù)為 70°70°．
【答案】-16；70°
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/20 8:0:8組卷：269引用：1難度：0.5
相似題
-
1．若x,y是等腰三角形的兩條邊，且滿足4x2+17y2-16xy-4y+4=0，求△ABC的周長(zhǎng)．
發(fā)布：2025/6/3 13:0:1組卷：72引用：3難度：0.6 -
2．仔細(xì)閱讀下列解題過程：
若a2+2ab+2b2-6b+9=0，求a、b的值．
解：∵a2+2ab+2b2-6b+9=0
∴a2+2ab+b2+b2-6b+9=0
∴（a+b）2+（b-3）2=0
∴a+b=0，b-3=0
∴a=-3，b=3
根據(jù)以上解題過程，試探究下列問題：
（1）已知x2-2xy+2y2-2y+1=0，求x+2y的值；
（2）已知a2+5b2-4ab-2b+1=0，求a、b的值；
（3）若m=n+4，mn+t2-8t+20=0，求n2m-t的值．發(fā)布：2025/6/3 20:0:2組卷：2996引用：10難度：0.3 -
3．閱讀下面的材料：
我們可以用配方法求一個(gè)二次三項(xiàng)式的最大值或最小值，例如：求代數(shù)式a2-2a+5的最小值．方法如下：
∵a2-2a+5=a2-2a+1+4=（a-1）2+4，由（a-1）2≥0，得（a-1）2+4≥4；
∴代數(shù)式a2-2a+5的最小值是4．
（1）仿照上述方法求代數(shù)式x2+10x+7的最小值；
（2）代數(shù)式-a2-8a+16有最大值還是最小值？請(qǐng)用配方法求出這個(gè)最值．發(fā)布：2025/6/3 16:30:1組卷：935引用：12難度：0.5