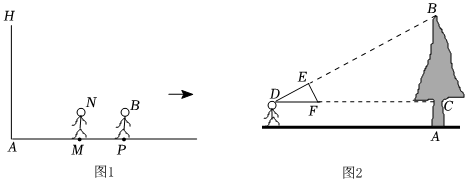
我國古代數學家趙爽利用影子對物體進行測量的方法，至今仍有借鑒意義．如圖1，身高1.5m的小王晚上在路燈燈柱AH下散步，他想通過測量自己的影長來估計路燈的高度，具體做法如下：先從路燈底部A向東走20步到M處，發現自己的影子端點落在點P處，作好記號后，繼續沿剛才自己的影子走4步恰好到達點P處，此時影子的端點在點Q處，已知小王和燈柱的底端在同一水平線上，小王的步間距保持一致．
（1）請在圖中畫出路燈O和影子端點Q的位置．
（2）估計路燈AO的高，并求影長PQ的步數．
（3）無論點光源還是視線，其本質是相同的，日常生活中我們也可以直接利用視線解決問題．如圖2，小明同學用自制的直角三角形紙板DEF測量樹的高度AB，他調整自己的位置，設法使斜邊DF保持水平，并且邊DE與點B在同一直線上．測得DF=0.5m,EF=0.3m,CD=10m,小明眼睛到地面的距離為1.5m,則樹高AB為 99m.
【答案】9
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：120引用：3難度：0.5
相似題
-
1．在3×3的正方形格點圖中有格點△ABC，請在下圖1～3中分別按下列要求畫出一個不同于△ABC的格點三角形．
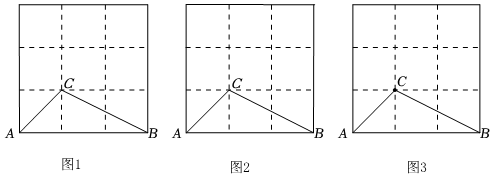
（1）在圖1中畫出的格點△ABD，且與△ABC面積相等．
（2）在圖2中畫出的格點△ACE，且與△ABC面積相等．
（3）在圖3中畫出的格點△BCF，且是一個軸對稱圖形．發布：2024/12/23 16:30:2組卷：47引用：3難度：0.6 -
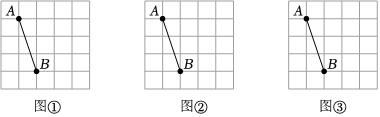
2．如圖，圖①、圖②、圖③均是5×5的正方形網格，每個小正方形的邊長均為1，其頂點稱為格點，點A、B均在格點上，只用無刻度的直尺，在圖①、圖②、圖③中，分別畫一個等腰三角形ABC，要求點C在格點上，三個圖形中的等腰三角形ABC位置不相同，但均為銳角三角形．
發布：2025/5/21 10:30:2組卷：85引用：1難度：0.5 -
3．如圖，在每個小正方形的邊長為1的網格中，△ABC的頂點A，B，C均落在格點上，以AB為直徑的半圓的圓心為O，僅用無刻度的直尺在給定網格中完成畫圖：
（1）請在圖1中作出△ABC的AC邊上的高BD；
（2）請在圖2中線段BC上確定一點F，使得OF∥AC；
（3）請在圖3中作出⊙O的切線AE．
發布：2025/5/21 14:0:2組卷：560引用：8難度：0.5