某工廠計劃生產(chǎn)A，B兩種產(chǎn)品共10件，其生產(chǎn)成本和利潤如下表：
| A種產(chǎn)品 | B種產(chǎn)品 | |
| 成本（萬元∕件） | 3 | 5 |
| 利潤（萬元∕件） | 1 | 2 |
（2）若工廠投入資金不多于44萬元，且獲利多于14萬元，問工廠有哪幾種生產(chǎn)方案？
（3）在（2）條件下，哪種方案獲利最大？并求最大利潤．
【考點(diǎn)】一元一次不等式組的應(yīng)用；二元一次方程組的應(yīng)用．
【答案】見試題解答內(nèi)容
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：704引用：20難度：0.5
相似題
-
1．一個數(shù)位大于等于4的多位數(shù)n,規(guī)定其末三位數(shù)與末三位數(shù)以前的數(shù)字所組成的數(shù)之差記為F（n），則
=；若F（n）能被11整除，則這個多位數(shù)就一定能被11整除，反之，一個數(shù)位大于等于4的多位數(shù)n能被11整除，則n的末三位數(shù)與末三位數(shù)以前的數(shù)字所組成的數(shù)之差F（n）一定能被11整除．若兩個四位數(shù)s,t,其中s能被11整除，且s=2000a+321，t的千位數(shù)字為b-2，百位數(shù)字為4，十位數(shù)字為3，個位數(shù)字為c-3（a,b,c均為整數(shù)），規(guī)定F（739882）11，當(dāng)K（s,t）=a+bc時，則K（s,t）的最小值為 ．F（t）11-F（s）11=10發(fā)布：2025/5/22 7:30:2組卷：494引用：6難度：0.6 -
2．每年的4月23日為“世界讀書日”．為了迎接第28個世界讀書日，我市圖書館決定購買甲、乙兩種品牌的平板電腦若干組建新的電子閱覽室．經(jīng)了解，甲、乙兩種品牌的平板電腦單價分別2400元和3600元．
（1）若購買甲、乙兩種品牌的平板電腦共50臺，恰好支出144000元，求甲、乙兩種品牌的平板電腦各購買了多少臺？
（2）若購買甲、乙兩種品牌的平板電腦共50臺，每種品牌至少購買一臺，且支出不超過124000元，共有幾種購買方案？并說明哪種方案最省錢．發(fā)布：2025/5/21 20:0:2組卷：844引用：2難度：0.7 -
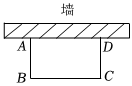3．如圖，用40m長的籬笆圍成一邊靠墻（墻足夠長）的矩形ABCD菜園，若6m≤AB≤10m,則BC的取值范圍為 ．發(fā)布：2025/5/21 20:30:1組卷：568引用：4難度：0.6
相關(guān)試卷