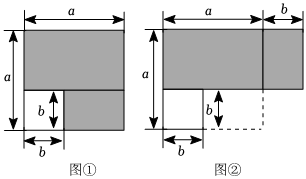
如圖①，從邊長為a的大正方形中剪掉一個邊長為b的小正方形，將陰影部分沿線剪開，如圖所示，拼成圖②的長方形．
（1）【探究】
①請你分別表示出這兩個圖形中陰影部分的面積 a2-b2a2-b2； （a+b）（a-b）（a+b）（a-b）；
②比較兩圖的陰影部分面積，可以得到乘法公式：（a+b）（a-b）=a2-b2（a+b）（a-b）=a2-b2（用字母表示）；
（2）【應用】請應用這個公式完成計算：2001×1999．
【考點】平方差公式的幾何背景；完全平方公式的幾何背景．
【答案】a2-b2；（a+b）（a-b）；（a+b）（a-b）=a2-b2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/31 14:30:1組卷：348引用：2難度：0.6
相似題
-
1．（1）如圖1所示，若大正方形的邊長為a,小正方形的邊長為b,則陰影部分的面積是 ；若將圖1中的陰影部分裁剪下來，重新拼成如圖2所示的一個長方形，則它的面積是 ；
（2）由（1）可以得到一個公式：；
（3）利用你得到的公式計算：20212-2022×2020．
發布：2025/6/1 12:30:1組卷：371引用：2難度：0.7 -
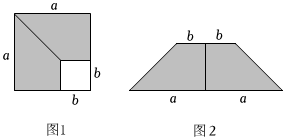2．在邊長為a的正方形上剪去一個邊長為b的小正方形（a＞b），如圖1，把余下的部分拼成一個梯形，如圖2，根據這兩個圖形的陰影部分面積關系，可以驗證的等式是（ ）發布：2025/6/2 3:30:1組卷：17引用：2難度：0.7 -
3．如圖1，從邊長為a的正方形剪掉一個邊長為b的正方形；如圖2，然后將剩余部分拼成一個長方形，上述操作能驗證的等式是（ ）發布：2025/6/1 18:30:1組卷：108引用：3難度：0.6