（1）問題發現
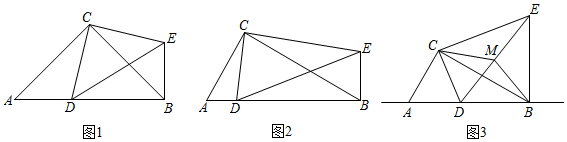
如圖1，在Rt△ABC和Rt△CDE中，∠ACB=∠DCE=90°，∠CAB=∠CDE=45°，點D是線段AB上一動點，連接BE．
填空：
①BEAD的值為 11；
②∠DBE的度數為 90°90°．
（2）類比探究
如圖2，在Rt△ABC和Rt△CDE中，∠ACB=∠DCE=90°，∠CAB=∠CDE=60°，點D是線段AB上一動點，連接BE．請判斷BEAD的值及∠DBE的度數，并說明理由．
（3）拓展延伸
如圖3，在（2）的條件下，將點D改為直線AB上一動點，其余條件不變，取線段DE的中點M，連接BM、CM，若AC=2，則當△CBM是直角三角形時，線段BE的長是多少？請直接寫出答案．
BE
AD
BE
AD
【考點】相似形綜合題．
【答案】1；90°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：3049引用：24難度：0.2
相似題
-
1．如圖1，在Rt△ABC中，∠BAC=90°，D為邊AB上一點，∠ACD=∠B．
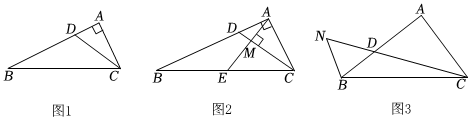
（1）求證：AC2=AD?AB；
（2）如圖2，過點A作AM⊥CD于M，交BC于點E，若AB=4AD，求的值；AMME
（3）如圖，N為CD延長線上一點，連接BN，且∠NBD=2∠ACD，若，直接寫出tan∠ACD=1n（n＞1）的值（用含n的代數式表示）．NDDC發布：2025/5/22 10:30:1組卷：557引用：4難度：0.1 -
2．問題背景：某學習小組正在研究如下問題：如圖1所示，四邊形ABCD與四邊形CEFG均為正方形，且點E、G分別在邊BC、CD上，連接DE、BG，點M是BG中點，連接CM，試猜測CM與DE的數量關系與位置關系，并加以證明．
解決問題：小華從旋轉的角度提出一個問題：如圖2，將正方形CEFG繞點C順時針旋轉一定角度，其他條件不變，此時“問題背景”中的結論還成立嗎？如果成立，請加以證明；如果不成立，請說明理由．
拓展延伸：小剛提出了一個更加一般化的問題：如圖3所示，?ABCD∽?ECGF，且，其他條件不變，此時CM與DE又有怎樣的數量關系？請直接寫出結果．ABBC=ab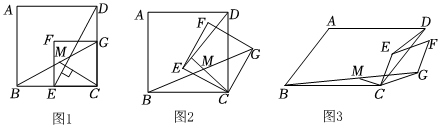
?發布：2025/5/22 10:30:1組卷：242引用：4難度：0.1 -
3．如圖，在Rt△ABC中，∠ACB=90°，AC=6，BC=3．點D是邊AC上一動點（不與A、C重合），聯結BD，過點C作CF⊥BD，分別交BD、AB于點E、F．
（1）當CD=2時，求∠ACF的正切值；
（2）設CD=x,，求y關于x的函數解析式，并寫出x的定義域；AFBF=y
（3）聯結FD并延長，與邊BC的延長線相交于點G，若△DGC與△BAC相似，求的值．AFBF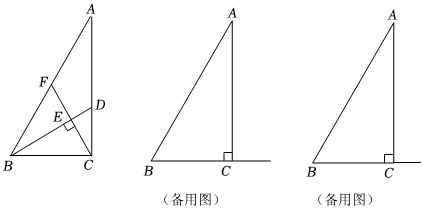
發布：2025/5/22 11:30:2組卷：530引用：1難度：0.4