在學習平行四邊形時，我們先學習了平行四邊形的性質定理、判定定理，再通過平行四邊形邊、角的特殊化，獲得了特殊的平行四邊形——矩形、菱形和正方形，了解了它們之間的關系，并根據它們的特殊性，得到了這些特殊的平行四邊形的性質定理和判定定理．在學習這些知識的過程中，主要體現的數學思想是（　　）

A．方程思想	B．數形結合思想
C．從特殊到一般思想	D．從一般到特殊思想

【答案】D

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/5/29 8:0:9組卷：34引用：3難度：0.7

相似題

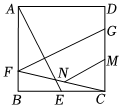
1．如圖，在邊長為3的正方形ABCD中，點E在邊AD上，且DE=1．△BEF是以E為直角頂點的等腰直角三角形，EF，BF分別交CD于點M，N，過點F作AD的垂線交AD的延長線于點G．連接DF，則下列結論錯誤的是（　　）
A．
EF
=
13
B．
DF
=
2
2
C．
CN
=
3
5
D．
MN
=
5
3
發布：2025/5/23 17:0:1組卷：266引用：3難度：0.5
解析
2．如圖，點E為正方形ABCD的邊BC的中點，連接AE，點F、G分別為AB、CD上的點，連接FG，CF，取CG、CF的中點M、N，連接MN，已知正方形的邊長為4，若FG⊥AE，則MN的長為
．
發布：2025/5/23 17:30:1組卷：326引用：2難度：0.5
解析
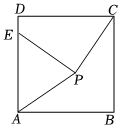3．如圖，點E在正方形ABCD的AD邊上，P為該正方形內一點，PA=PC=PE．請完成下列問題：
（1）若∠APE=70°，則∠PCD=
；
（2）若
DE
AE
=
1
4
，則
PA
AB
的值為
．
發布：2025/5/23 17:30:1組卷：167引用：3難度：0.5
解析

相關試卷

1．如圖，在邊長為3的正方形ABCD中，點E在邊AD上，且DE=1．△BEF是以E為直角頂點的等腰直角三角形，EF，BF分別交CD于點M，N，過點F作AD的垂線交AD的延長線于點G．連接DF，則下列結論錯誤的是（ ）