2022-2023學年山西省呂梁市孝義市八年級（下）期中數學試卷

一、選擇題（每小題3分，共30分．下列各小題均給出四個備選答案，請將符合題意選項的字母代號，填寫在下面方格內）

• 1．若二次根式

  2

  -

  a

  在實數范圍內有意義，則a的取值范圍是（　　）

  A．a≥0

  B．a＜2

  C．a≥2

  D．a≤2
  組卷：150引用：3難度：0.5

  解析

• 2．下列二次根式中，可以與

  2

  合并的是（　　）

  A． 0 . 2

  B． 1 2

  C． 12

  D． 20
  組卷：724引用：6難度：0.5

  解析

• 3．下列計算正確的是（　　）

  A． 2 + 3 = 2 3

  B． 5 - 3 = 2

  C． 2 2 × 3 = 2 6

  D． 4 2 ÷ 2 2 = 2 2
  組卷：87引用：5難度：0.7

  解析

• 4．下列各組數中不能作為直角三角形三邊長的是（　　）

  A．1.5，2，3

  B．7，24，25

  C．8，15，17

  D．9，12，15
  組卷：53引用：3難度：0.5

  解析

• 5．如圖，在△ABC中，∠ACB=90°，AC=3，BC=1，AC在數軸上，點A所表示的數為1，以點A為圓心，AB長為半徑畫弧，在點A左側交數軸于點D，則點D表示的數是（　　）

  A． 10

  B． - 10

  C． 1 - 10

  D． 10 - 1
  組卷：194引用：5難度：0.6

  解析

• 6．如圖，在?ABCD中，對角線AC、BD相交于點O，過點O作OE⊥BD交AD于點E，連接BE．若?ABCD的周長為20，則△ABE的周長為（　　）

  A．5

  B．10

  C．15

  D．20
  組卷：753引用：9難度：0.6

  解析

• 7．在學習平行四邊形時，我們先學習了平行四邊形的性質定理、判定定理，再通過平行四邊形邊、角的特殊化，獲得了特殊的平行四邊形——矩形、菱形和正方形，了解了它們之間的關系，并根據它們的特殊性，得到了這些特殊的平行四邊形的性質定理和判定定理．在學習這些知識的過程中，主要體現的數學思想是（　　）

  A．方程思想	B．數形結合思想
  C．從特殊到一般思想	D．從一般到特殊思想
  組卷：34引用：3難度：0.7

  解析

三、解答題（本大題共7個小題，共55分．解答題應寫出文字說明、證明過程或演算步驟）

• 21．請閱讀下列材料，并完成相應任務．
  勾股定理的證明
  勾股定理揭示了直角三角形三條邊之間的數量關系，是數學中最重要的定理之一．勾股定理的證明過程多數采用的方法是“用兩種不同的方法和含有a,b,c的式子表示同一個圖形的面積”，由于同一個圖形的面積相等，從而得到含a,b,c的恒等式，通過化簡即可完成勾股定理的證明．借助于圖形的面積研究相關的數量關系，是我國古代數學研究中經常采用的重要方法，它充分顯示了古人的卓越智慧．
  下面是證明勾股定理的一種思路：
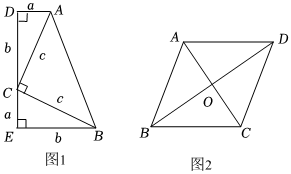
  如圖1，用一個等腰直角三角形（Rt△ABC），和兩個全等的直角三角形（Rt△ACD，Rt△BCE）可以拼成一個直角梯形ABED．其中AD=CE=a；CD=BE=b,AC=BC=c,用兩種不同的方法和含有a,b,c的式子表示梯形ABED的面積，就能完成勾股定理的證明．
  提示：梯形的面積

  S

  =

  1

  2

  ×

  （上底+下底）×高
  任務：
  （1）請你根據上述材料中的思路證明勾股定理；
  （2）如圖2，在菱形ABCD中，對角線AC、BD相交于點O，AC=12，BD=16，則AD、BC之間的距離為

  ．
  組卷：60引用：2難度：0.5

  解析

• 22．綜合與實踐
  實踐操作：如圖1，已知矩形紙片ABCD．
  第一步：如圖2，將紙片沿AE折疊，使點B的對應點B′正好落在AD上，然后展平紙片，得到折痕AE；
  第二步：如圖3，在圖2的基礎上，沿DE折疊紙片，點C的對應點落在C′處，C′D與EB′交于點F．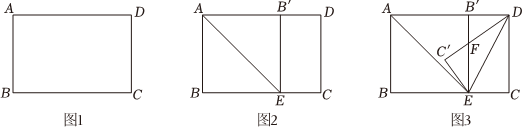
  
  問題解決：
  （1）如圖2，判斷四邊形ABEB′的形狀，并證明；
  （2）如圖3，證明B′F=C′F；
  （3）若AB=4，BC=6，則△DEF的周長為

  （直接寫出答案即可）．
  組卷：101引用：3難度：0.5

  解析