（1）用“＜”、“＞”、“=”填空：
52+32＞＞2×5×3
32+32==2×3×3
（-3）2+22＞＞2×（-3）×2
（-4）2+（-4）2==2×（-4）×（-4）
（2）觀察以上各式，你發現它們有什么規律嗎？用一個含有字母的式子表示上述規律．
【考點】規律型：數字的變化類．
【答案】＞；=；＞；=
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/8 17:30:2組卷：126引用：3難度：0.7
相似題
-
1．觀察下列各式：
，11×3=12×（1-13），13×5=12×（13-15），…，15×7=12×（15-17），…199×101=12×（199-1101）
計算下列各題：；（1）11×3+13×5+15×7+?+199×101．（2）12×6+16×10+110×14+?+12018×2022發布：2025/6/8 22:30:1組卷：84引用：1難度：0.6 -
2．如圖是關于數學的一個趣味游戲，也稱“3x+1問題”，小明一開始輸入的數字是13，第一次輸出的結果為40，第二次輸出的結果為20，……，請問第100次輸出的結果為 ．
發布：2025/6/9 1:30:1組卷：31引用：1難度：0.6 -
3．已知n≥2，且n為自然數，對n2進行如下“分裂”，可分裂成n個連續奇數的和，如圖：
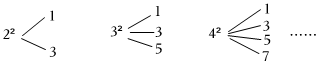
即如下規律：22=1+3，32=1+3+5，42=1+3+5+7，……
（1）按上述分裂要求，將5分裂成奇數和的形式：52=；102可分裂的最大奇數為 ；
（2）按上述分裂要求，n2可分裂成連續奇數和的形式是：n2=1+3+5+…+（填最大奇數，用含n的式子表示）；
（3）用上面的規律求：（n+1）2-n2．發布：2025/6/9 0:0:2組卷：111引用：4難度：0.5