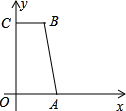
如圖，在直角坐標系中，直角梯形OABC的頂點A（3，0）、B（2，7），P為線段OC上一點，若過B、P兩點的直線為y₁=k₁x+b₁，過A、P兩點的直線為y₂=k₂x+b₂，且BP⊥AP，則k₁k₂（k₁+k₂）=
-
8
3
或
3
2
-
8
3
或
3
2
．

【答案】-

或

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/5/27 14:0:0組卷：262引用：5難度：0.9

相似題

1．如圖，在△ABC中，AB=9，BC=8，CA=7，延長BC至P，使△PAB∽△PCA，則PC=

．
發布：2025/5/27 9:30:1組卷：95引用：1難度：0.5
解析
2．已知如圖，矩形ABCD中，E、F分別是邊BC、CD上的點，AB=4，AD=8，CF=3，若△ABE與以E、C、F為頂點的三角形相似，則BE的長為
．
發布：2025/5/27 18:0:1組卷：762引用：6難度：0.5
解析
3．如圖，在等腰梯形ABCD中，∠B=60°，且AB=AD=CD，請你將等腰梯形分成3個三角形，使得其中有兩個是相似三角形，且相似比不為1．
現在請你參考示意圖，另外再給出三種分割方法（注：在兩個相似三角形中標明必要的角度．）
發布：2025/5/27 19:30:1組卷：498引用：4難度：0.1
解析

相關試卷

如圖，在直角坐標系中，直角梯形OABC的頂點A（3，0）、B（2，7），P為線段OC上一點，若過B、P兩點的直線為y1=k1x+b1，過A、P兩點的直線為y2=k2x+b2，且BP⊥AP，則k1k2（k1+k2）=-83或32-83或32．