考古學家在考古過程中發現一個圓盤，但是因為歷史悠久，已經有一部分缺失，現希望復原圓盤，需要先找到圓盤的圓心，才能繼續完成后續修復工作．在如圖1所示的圓盤邊緣上任意找三個點A，B，C．
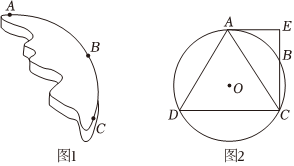
（1）請利用直尺（無刻度）和圓規，在圖1中畫出圓心O．（要求：不寫作法，保留作圖痕跡）
（2）如圖2，數學興趣小組的同學在（1）的基礎上，補全⊙O，連接AC，BC，過點A作⊙O的切線交CB的延長線于點E，過點C作CD∥AE，交⊙O于點D，連接AD．
①求證：AD=AC；
②連接DB，若DB為⊙O的直徑，AC=70，BC=4，求⊙O的半徑．
70
【考點】圓的綜合題．
【答案】（1）圖形見解析；
（2）①證明見解析；
②5．
（2）①證明見解析；
②5．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/9 8:0:9組卷：178引用：2難度：0.5
相似題
-
1．閱讀下列材料，并解答后面的問題．
在學習了直角三角形的邊角關系后，小穎和小明兩個學習小組繼續探究任意銳角三角形的邊角關系：在銳角△ABC中，∠A、∠B、∠C的對邊分別是a、b、c.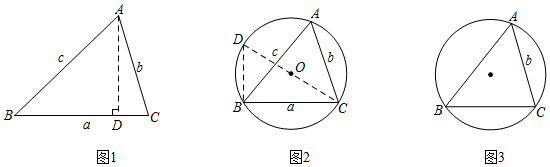
（1）小明學習小組發現如下結論：
如圖1，過A作AD⊥BC于D，則sinB=，sinC=ADc，即AD=csinB，AD=bsinC，于是 =，即ADb=bsinB，同理有csinC=csinC，asinA=asinA，bsinB
則有=asinA=bsinB．csinC
（2）小穎學習小組則利用圓的有關性質也得到了類似的結論：
如圖2，△ABC的外接圓半徑為R，連接CO并延長交⊙O于點D，連接DB，則∠D=∠A，
∵CD為⊙O的直徑，
∴∠DBC=90°，
在Rt△DBC中，
∵sinD=，BCDC=a2R
∴sinA=，即a2R=2R，asinA
同理：=2R，bsinB=2R，csinC
則有=2R，asinA=bsinB=csinC
請你將這一結論用文字語言描述出來：．
小穎學習小組在證明過程中略去了“=2R，bsinB=2R”的證明過程，請你把“csinC=2R，”的證明過程補寫出來．bsinB
（3）直接用前面閱讀材料中得出的結論解決問題
規劃局為了方便居民，計劃在三個住宅小區A、B、C之間修建一座學校，使它到三個住宅小區的距離相等，已知小區C在小區B的正東方向千米處，小區A在小區B的東北方向，且A與C之間相距3千米，求學校到三個小區的距離及小區A在小區C的什么方向？2發布：2025/5/25 6:30:1組卷：296引用：2難度：0.4 -
2．有一組鄰邊相等且對角互補的四邊形叫做等鄰邊互補四邊形．
（1）如圖1，在等鄰邊互補四邊形ABCD中，AD=CD，且AD∥BC，BC=2AD，則∠B=．
（2）如圖2，在等鄰邊互補四邊形ABCD中，∠BAD=90°，且BC=CD，求證：AB+AD=AC．2
（3）如圖3，四邊形ABCD內接于⊙O，連結DO并延長分別交AC，BC于點E，F，交⊙O于點G，若點E是AC的中點，，tan∠ABC=?AB=?BG，AC=6，求FG的長．247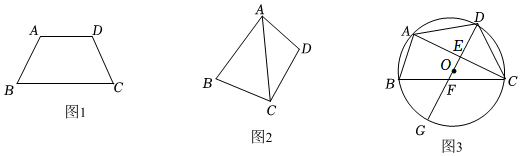
發布：2025/5/25 6:30:1組卷：647引用：3難度：0.2 -
3．【問題提出】
（1）如圖1，在矩形ABCD中，AD=10，AB=12，點E為AD的中點，點P為矩形ABCD內以BC為直徑的半圓上一點，則PE的最小值為 ；
【問題探究】
（2）如圖2，在△ABC中，AD為BC邊上的高，且AD=BC=4，點P為△ABC內一點，當時，求PB+PC的最小值；S△PBC=12S△ABC
【問題解決】
（3）李伯伯家有一塊直角三角形菜園ABC，如圖3，米，∠C=90°，∠ABC=60°，李伯伯準備在該三角形菜園內取一點P，使得∠APB=120°，并在△ABP內種植當季蔬菜，邊BC的中點D為菜園出入口，為了種植方便，李伯伯打算在AC邊上取點E，并沿PE、DE修兩條人行走道，為了節省時間，要求人行走道的總長度（PE+DE）盡可能小，問PE+DE的長度是否存在最小值？若存在，求出其最小值；若不存在，請說明理由．BC=2003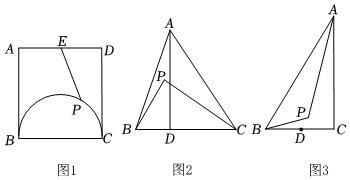
發布：2025/5/25 7:0:2組卷：367引用：4難度：0.3
相關試卷