當(dāng)前位置:
2022-2023學(xué)年江蘇省揚(yáng)州市寶應(yīng)縣開發(fā)區(qū)國際學(xué)校聯(lián)盟校九年級(下)月考數(shù)學(xué)試卷(3月份)>
試題詳情
如果一個(gè)四邊形的對角線相等,我們稱這個(gè)四邊形為美好四邊形.
【問題提出】
(1)如圖①,點(diǎn)E是四邊形ABCD內(nèi)部一點(diǎn),且滿足EB=EC,EA=ED,∠BEC=∠AED,請說明四邊形ABCD是美好四邊形;
【問題探究】
(2)如圖②,△ABC,請利用尺規(guī)作圖,在平面內(nèi)作出點(diǎn)D使得四邊形ABCD是美好四邊形,且滿足AD=BD.保留作圖痕跡,不寫畫法;
(3)在(2)的條件下,若圖②中△ABC滿足:∠ABC=90°,AB=4,BC=3,求四邊形ABCD的面積;
【問題解決】
(4)如圖③,某公園內(nèi)需要將4個(gè)信號塔分別建在A、B、C、D四處,現(xiàn)要求信號塔C建在公園內(nèi)一個(gè)湖泊的邊上,該湖泊可近似看成一個(gè)半徑為200m的圓,記為⊙E.已知點(diǎn)A到該湖泊的最近距離為500m,是否存在這樣的點(diǎn)D,滿足AC=BD,且使得四邊形ABCD的面積最大?若存在,求出最大值;若不存在,請說明理由.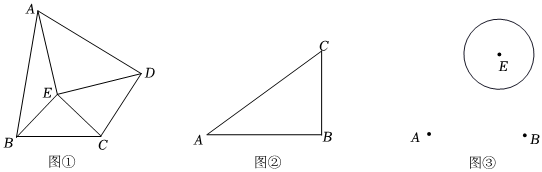
【考點(diǎn)】圓的綜合題.
【答案】(1)說明四邊形ABCD是美好四邊形見解答過程;
(2)作圖見解答過程;
(3)四邊形ABCD的面積為2+3;
(4)存在這樣的點(diǎn)D,滿足AC=BD,且使得四邊形ABCD的面積最大,四邊形ABCD的面積最大為405000m2.
(2)作圖見解答過程;
(3)四邊形ABCD的面積為2
21
(4)存在這樣的點(diǎn)D,滿足AC=BD,且使得四邊形ABCD的面積最大,四邊形ABCD的面積最大為405000m2.
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2025/5/25 3:30:2組卷:216引用:2難度:0.1
相似題
-
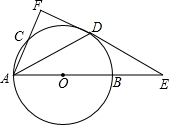 1.如圖,AB是⊙O的直徑,點(diǎn)C是⊙O上一點(diǎn),點(diǎn)D是的中點(diǎn),過點(diǎn)D作⊙O的切線,與AB、AC的延長線分別交于點(diǎn)E、F,連接AD.?BC
1.如圖,AB是⊙O的直徑,點(diǎn)C是⊙O上一點(diǎn),點(diǎn)D是的中點(diǎn),過點(diǎn)D作⊙O的切線,與AB、AC的延長線分別交于點(diǎn)E、F,連接AD.?BC
(1)求證:AF⊥EF.
(2)填空:
①已知AB=8,當(dāng)BE=時(shí),AC=CF.
②連接BD、CD、OC.當(dāng)∠E的度數(shù)為時(shí),四邊形OBDC是菱形.發(fā)布:2025/5/25 9:0:1組卷:173引用:2難度:0.4 -
 2.已知扇形OAB的半徑為4,∠AOB=90°,點(diǎn)P是OA的中點(diǎn),點(diǎn)Q是弧AB上的一個(gè)動點(diǎn),如圖1,將扇形沿PQ折疊,點(diǎn)A的對應(yīng)點(diǎn)為A',連接AA'.
2.已知扇形OAB的半徑為4,∠AOB=90°,點(diǎn)P是OA的中點(diǎn),點(diǎn)Q是弧AB上的一個(gè)動點(diǎn),如圖1,將扇形沿PQ折疊,點(diǎn)A的對應(yīng)點(diǎn)為A',連接AA'.
(1)如圖2,當(dāng)點(diǎn)O與點(diǎn)A'重合時(shí),求弧BQ的長.
(2)在點(diǎn)Q的運(yùn)動過程中,求點(diǎn)A′與點(diǎn)B之間的最小距離.
(3)如圖3,當(dāng)Q是弧AB上的中點(diǎn)時(shí),求tan∠APQ的值.發(fā)布:2025/5/25 8:30:2組卷:146引用:2難度:0.5 -
3.如圖,Q是
上一定點(diǎn),P是弦AB上一動點(diǎn),C為AP中點(diǎn),連接CQ,過點(diǎn)P作PD∥CQ交?AB于點(diǎn)D,連接AD,CD.已知AB=8cm,設(shè)A,P兩點(diǎn)間的距離為xcm,C,D兩點(diǎn)間的距離為ycm.(當(dāng)點(diǎn)P與點(diǎn)A重合時(shí),令y的值為1.30)?AB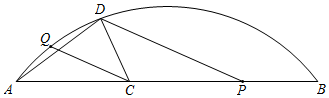
小榮根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),對函數(shù)y隨自變量x的變化而變化的規(guī)律進(jìn)行了探究.
下面是小榮的探究過程,請補(bǔ)充完整:
(1)按照下表中自變量x的值進(jìn)行取點(diǎn)、畫圖、測量,得到了y與x的幾組對應(yīng)值:
(2)建立平面直角坐標(biāo)系,描出以補(bǔ)全后的表中各組對應(yīng)值為坐標(biāo)的點(diǎn),畫出該函數(shù)的圖象;x/cm 0 1 2 3 4 5 6 7 8 y/cm 1.30 1.79 1.74 1.66 1.63 1.69 2.08 2.39 
(3)結(jié)合函數(shù)圖象,解決問題:當(dāng)DA⊥DP時(shí),AP的長度約為cm.發(fā)布:2025/5/25 9:30:1組卷:358引用:3難度:0.1


