易見1991=2×45+0×44+（-1）×43+0×42+2×41+（-1）×1．這個表達式的特點是：右邊1、41、42、43、…的若干倍之和，這里的倍數都是-1倍、0倍、1倍或者2倍，而4的最高次的倍數不足0倍．為此，我們把這個表達式簡寫成1991=（2，0，-1，0，2，-1）4．現在，如果需要把倍數改為-2倍、-1倍、0倍或1倍，而其他方式和意義均不改變，則表達式應改寫為1991=（-（-2），0，-1，1，-2，-1-（-2），0，-1，1，-2，-1）4．
【考點】整數問題的綜合運用．
【答案】-（-2），0，-1，1，-2，-1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：35引用：1難度：0.5
相似題
-
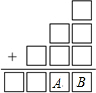1．在右邊的加法算式中，每一個□表示一個數字，任意兩個數字都不相同，那么A與B乘積的最大值是．發布：2025/5/28 16:0:1組卷：41引用：1難度：0.5 -
2．x,y為正整數，且兩個分數之和
也是整數，求證：這兩個分數都是整數．x2-1y+1+y2-1x+1發布：2025/5/28 16:0:1組卷：66引用：1難度：0.1 -
3．已知下面等式對任意實數x都成立（n為正整數）：（1+x）+（1+x）2+（1+x）3+…+（1+x）n=a0+a1x+a2x2+…+anxn，且a1+a2+a3+…+an=57，則滿足條件的n的可能值是
．發布：2025/5/28 16:30:2組卷：78引用：2難度：0.5