(1)回歸教材:如圖1所示,點P是直線m外一點,PO⊥m,點O是垂足,點A、B、C在直線m上,比較線段PO,PA,PB,PC的長短,你發現了什么?
最短線段是 POPO,于是,小明這樣總結:直線外一點與直線上各點連接的所有線段中,垂線段最短垂線段最短.
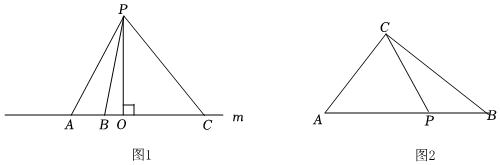
(2)小試牛刀:如圖2所示,Rt△ABC中,∠ACB=90°,AB=5,AC=4.則點P為AB邊上一動點,則CP的最小值為 2.42.4.
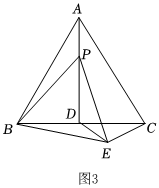
(3)嘗試應用:如圖3所示△ABC是邊長為4的等邊三角形,其中點P為高AD上的一個動點,連接BP,將BP繞點B順時針旋轉60°得到BE,連接PE、DE、CE.
①求出DE的最小值.
②在①的條件下求△BPE的面積.
【考點】幾何變換綜合題.
【答案】PO;垂線段最短;2.4
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:352引用:1難度:0.2
相似題
-
1.如圖,過邊長為4的等邊△ABC的頂點A作直線l∥BC,點D在直線l上(不與點A重合),作射線BD,將射線BD繞點B順時針旋轉60°后交直線AC于點E.
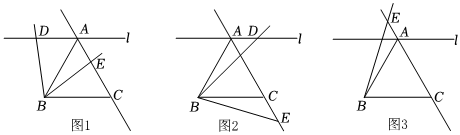
(1)如圖1,點D在點A的左側,點E在邊AC上,求證:AB=AD+AE.
(2)如圖2,點D在點A的右側,點E在邊AC的延長線上,那么(1)中的結論還成立嗎?若成立,請證明;若不成立,寫出你的結論,再證明.
(3)如圖3,點E在邊AC的反向延長線上,若∠ABE=15°,請直接寫出線段AD的長.發布:2025/6/4 4:0:2組卷:96引用:2難度:0.3 -
2.如圖1,在平面直角坐標系內,直線AB與x軸正半軸交于點A,與y軸正半軸交于點B,點C是x軸負半軸上一點,點D是直線AB上位于第四象限內的一點,直線MN經過原點O,且OM平分∠BOC,∠BAC的平分線與直線MN交于點E,∠CAD的平分線與直線MN交于點F.

(1)判斷AE與AF的位置關系,并說明理由;
(2)在∠EAF,∠AEF,∠AFE中,如果有一個角是另一個角的4倍,直接寫出∠ABO的度數:;
(3)如圖2,當∠ABO取(2)結論中的最大值時,過點A作AQ⊥AB交直線MN于點Q,點G是直線MN上一點且∠DAG=27°,現將∠BAC繞點A逆時針旋轉α度,(0<α<135)得到∠B'AC',射線AC'交直線MN于點H,∠HAD的平分線交直線MN于點P,在旋轉過程中,是否存在α,使得∠GAH+∠QAB'=∠QPA,若存在,請直線寫出a的值;若不存在,請說明理由.發布:2025/6/3 22:0:1組卷:128引用:1難度:0.3 -
3.如圖,BC為等邊△ABM的高,AB=5
,點P為射線BC上的動點(不與點B、C重合),連接AP,將線段AP繞點P逆時針旋轉60°,得到線段PD,連接MD,BD.2
(1)如圖①,當點P在線段BC上時,且D在射線BC上時,求證:BP=DP.
(2)如圖②,當點P在線段BC的延長線上時,求證:BP=MD.
(3)若點P在線段BC的延長線上,且∠BDM=30°時,請直接寫出線段AP的長度.發布:2025/6/4 0:30:2組卷:327引用:4難度:0.1


