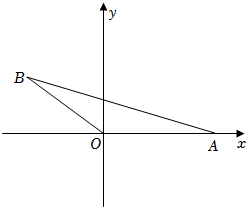
如圖，在平面直角坐標系中，點O為坐標原點，點A（6，0），B（m,n），其中m,n滿足2m-n=-11 3m+5n=3
，連接AB、OB．
（1）求點B的坐標．
（2）動點P以每秒2個單位長度的速度從點O出發，沿y軸正半軸勻速運動，設點P運動時間為t秒，請用含t的式子表示△ABP的面積．
（3）在（2）的條件下，在y軸負半軸取一點C，CP=10，點D是△AOP內部一點，連接PD、CD，CD與x軸交點F坐標（1，0），連接AD并延長交OP于點E，若∠EDP=45°，∠DEC=2∠EPD+∠ECD，當CF?AD=1031S△ABP時，求點P的坐標．
2 m - n = - 11 |
3 m + 5 n = 3 |
CF
?
AD
=
10
31
S
△
ABP
【考點】三角形綜合題．
【答案】（1）B（-4，3）；
（2）10t-9；
（3）點P的坐標為（0，8）．
（2）10t-9；
（3）點P的坐標為（0，8）．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/8 22:0:1組卷：144引用：1難度：0.3
相似題
-
1．[觀察發現]
①如圖1，△ABC中，AB=7，AC=5，點D為BC的中點，求AD的取值范圍．
小明的解法如下：延長AD到點E，使DE=AD，連接CE，易證△ABD≌△ECD（SAS）可得AB=CE，在△AEC中根據三角形三邊關系可得2＜AE＜12，又∵AE=2AD，∴1＜AD＜6．
②如圖2，在△ABC中，若AB=AC，則∠B=∠C；若∠B=∠C，則AB=AC．
[應用拓展]
如圖3，∠BCA=60°，∠AED=120°，CB=CA，EA=ED，連接CD，F為CD的中點，連接FB、FE．求證：BF⊥EF．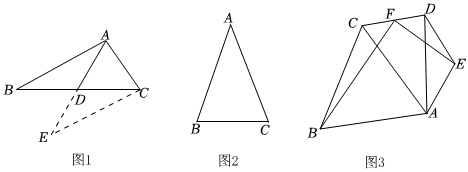
發布：2025/6/9 2:30:1組卷：109引用：2難度：0.3 -
2．已知，在平面直角坐標系中，A（a,0），B（b,0）為x軸上兩點，且a,b滿足：（a+3）2+（a+b）2=0，點C（0，
），∠ABC=30°，D為線段AB上一動點．3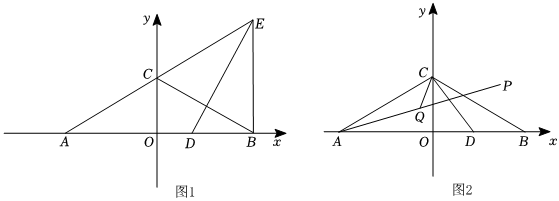
（1）則a=，b=．
（2）如圖1，若點D在BC的垂直平分線上，作∠ADE=120°，交AC的延長線于點E，連接BE，求證：BE⊥x軸；
（3）如圖2，作點D關于BC的對稱點P，連接AP，取AP中點Q，連接CQ、CD，求CQ的最小值．發布：2025/6/9 2:0:7組卷：263引用：1難度：0.4 -
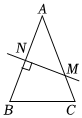3．如圖，在△ABC中，AB=AC，AB的垂直平分線交AB于N，交AC于M．
（1）若∠B=70°，則∠NMA的度數是 °．
（2）連接MB，若AB=8cm,△MBC的周長是14cm.
①求BC的長；
②點Q是線段BC上的動點，在直線MN上是否存在點P，使由BP+PQ最小？若存在，求BP+PQ的最小值；若不存在，說明理由．發布：2025/6/9 2:30:1組卷：27引用：1難度：0.3