合肥老城西大門有一處城門橫斷面分為兩部分,上半部分為拋物線形狀,下半部分為正方形(OMNE為正方形),已知城門寬度為4米,最高處離地面6米,如圖1所示,現(xiàn)以O(shè)點為原點,OM所在的直線為x軸,OE所在的直線為y軸建立直角坐標(biāo)系.
(1)求出上半部分拋物線的函數(shù)表達式,并寫出其自變量的取值范圍;
(2)有一輛寬3米,高4.5米的貨車需要通過該城門進入城區(qū),請問該貨車能否正常進入?
(3)由于城門年久失修,需要搭建一個矩形“鞏固門”ABCD,該“鞏固門”關(guān)于拋物線對稱軸對稱,如圖2所示,其中AB、AD、CD為三根承重鋼支架,點D在拋物線上,B、C在地面上,已知鋼支架每米300元,問搭建這樣一個矩形“鞏固門”,僅鋼支架一項,最多需要花費多少元?
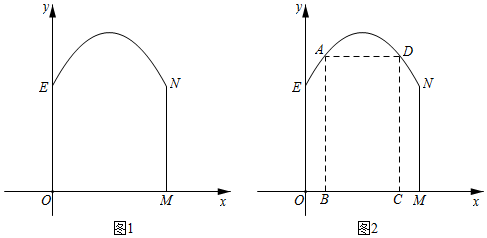
【考點】二次函數(shù)的應(yīng)用.
【答案】(1)y=-(x-2)2+6(0≤x≤4).
(2)貨車能正常駛?cè)耄?br />(3)3900元.
1
2
(2)貨車能正常駛?cè)耄?br />(3)3900元.
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:294引用:2難度:0.5
相似題
-
1.某公司以30元/千克的價格收購一批農(nóng)產(chǎn)品進行銷售,為了得到日銷售量p(千克)與銷售價格x(元/千克)之間的關(guān)系,經(jīng)過市場調(diào)查獲得部分?jǐn)?shù)據(jù)如表:
(1)請你根據(jù)表中的數(shù)據(jù),用所學(xué)過的一次函數(shù)、二次函數(shù)、反比例函數(shù)的知識確定p與x之間的函數(shù)表達式;銷售價格x(元/千克) 30 35 40 45 50 日銷售量p(千克) 600 450 300 150 0
(2)該公司應(yīng)該如何確定這批農(nóng)產(chǎn)品的銷售價格,才能使日銷售利潤最大?
(3)若該公司的日銷售利潤不低于2250元,應(yīng)該如何確定銷售價格?發(fā)布:2025/6/2 11:30:1組卷:172引用:3難度:0.5 -
2.某商店銷售一種成本為40元/千克的水產(chǎn)品,若按50元/千克銷售,一個月可售出500千克,銷售價每漲價1元,月銷售量就減少10千克.設(shè)售價為x(單位:元),月銷售量為y(單位:千克),月銷售利潤為W(單位:元).
(1)直接寫出y與x之間的函數(shù)解析式以及自變量x的取值范圍;
(2)當(dāng)月銷售利潤為6750元時,售價為多少元?
(3)當(dāng)售價定為多少元時月銷售利潤最大?并求出最大月銷售利潤.發(fā)布:2025/6/2 11:30:1組卷:250引用:3難度:0.5 -
3.某公司分別在A,B兩城生產(chǎn)同種產(chǎn)品,共100件.A城生產(chǎn)產(chǎn)品的總成本y(萬元)與產(chǎn)品數(shù)量x(件)之間具有函數(shù)關(guān)系y=ax2+bx.當(dāng)x=10時,y=400;當(dāng)x=20時,y=1000.B城生產(chǎn)產(chǎn)品的每件成本為70萬元.
(1)求a,b的值;
(2)當(dāng)A,B兩城生產(chǎn)這批產(chǎn)品的總成本的和最少時,求A,B兩城各生產(chǎn)多少件?
(3)從A城把該產(chǎn)品運往C,D兩地的費用分別為m萬元/件和3萬元/件;從B城把該產(chǎn)品運往C,D兩地的費用分別為1萬元/件和2萬元/件.C地需要90件,D地需要10件,在(2)的條件下,直接寫出A,B兩城總運費的和的最小值(用含有m的式子表示).發(fā)布:2025/6/2 14:0:1組卷:2561引用:8難度:0.4


