【閱讀材料】小明同學發現這樣一個規律：兩個頂角相等的等腰三角形，如果具有公共的頂點，并把它們的底角頂點連接起來則形成一組全等的三角形，小明把具有這個規律的圖形稱為“手拉手”圖形．如圖1，在“手拉手”圖形中，小明發現若∠BAC=∠DAE，AB=AC，AD=AE，則△ABD≌△ACE．
【材料理解】（1）在圖1中說明小明的發現；
【深入探究】（2）如圖2，△ABC和△AED是等邊三角形，連接BD、EC交于點O，連接AO，試說明：
①BD=EC；
②∠BOC=60°．
【考點】全等三角形的判定與性質；等邊三角形的性質．
【答案】證明過程見解答．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/13 8:0:9組卷：586引用：2難度：0.5
相似題
-
1．在△ABC中，高AD和BE所在的直線交于點H，且BH=AC，則∠ABC等于（ ）
發布：2025/6/25 5:30:3組卷：3235引用：5難度：0.3 -
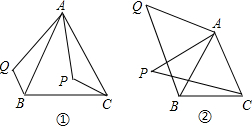2．復習“全等三角形”的知識時，老師布置了一道作業題：“如圖①，已知在△ABC中，AB=AC，P是△ABC內部任意一點，將AP繞A順時針旋轉至AQ，使得∠QAP=∠BAC，連接BQ、CP，則BQ=CP．”
（1）小亮是個愛動腦筋的同學，他通過對圖①的分析，證明了△ABQ≌△ACP，從而證得BQ=CP．請你幫小亮完成證明．
（2）之后，小亮又將點P移到等腰三角形ABC之外，原題中的條件不變，“BQ=CP”仍然成立嗎？若成立，請你就圖②給出證明．若不成立，請說明理由．發布：2025/6/25 8:0:1組卷：215引用：5難度：0.5 -
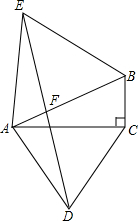3．已知：如圖，在Rt△ABC中，∠C=90°，∠A=30°，分別以AB、AC為邊在△ABC的外側作等邊△ABE和等邊△ACD，DE與AB交于F，
求證：EF=FD．發布：2025/6/25 8:0:1組卷：297引用：2難度：0.5