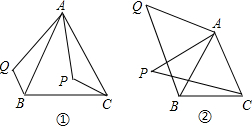
復習“全等三角形”的知識時，老師布置了一道作業題：“如圖①，已知在△ABC中，AB=AC，P是△ABC內部任意一點，將AP繞A順時針旋轉至AQ，使得∠QAP=∠BAC，連接BQ、CP，則BQ=CP．”
（1）小亮是個愛動腦筋的同學，他通過對圖①的分析，證明了△ABQ≌△ACP，從而證得BQ=CP．請你幫小亮完成證明．
（2）之后，小亮又將點P移到等腰三角形ABC之外，原題中的條件不變，“BQ=CP”仍然成立嗎？若成立，請你就圖②給出證明．若不成立，請說明理由．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/4/20 14:35:0組卷：213引用：5難度：0.5

相似題

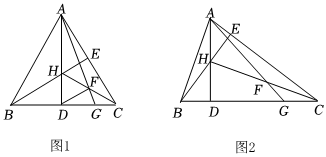1．在△ABC中，BC=8，兩條高AD，BE交于點H，F是CH的中點，連接AF并延長交邊BC于點G．
（1）如圖1，若△ABC是等邊三角形，
①求證：AH=2DH；
②求CG的長；
（2）如圖2，若AH=DH，CG=BD，求△ABC的面積．
發布：2025/5/30 14:30:1組卷：587引用：1難度：0.4
解析
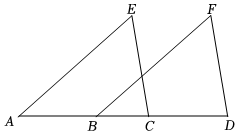2．已知：如圖，點A、B、C、D在一條直線上，EA∥FB，EA=FB，AB=CD．
①求證：EC=FD；
②若∠A=40°，∠D=80°，求∠E的度數．
發布：2025/5/30 14:30:1組卷：163引用：5難度：0.5
解析
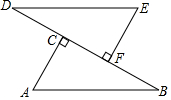3．如圖，D、C、F、B四點在一條直線上，AB=DE，AC⊥BD，EF⊥BD，垂足分別為點C、點F，CD=BF．求證：AB∥DE．
發布：2025/5/30 14:0:1組卷：1192引用：10難度：0.5
解析

相關試卷

1．在△ABC中，BC=8，兩條高AD，BE交于點H，F是CH的中點，連接AF并延長交邊BC于點G．（1）如圖1，若△ABC是等邊三角形，①求證：AH=2DH；②求CG的長；（2）如圖2，若AH=DH，CG=BD，求△ABC的面積．