已知：AD，CE都是銳角△ABC的高．
（1）如圖1，求證：∠B=∠CAD+∠ACE；
（2）如圖2，延長CE至F，使CF=AB，連接AF，BF，過點C作CG⊥BF于點G，在CG上取點M，使CM=BF，連接FM，求證：AF=FM；
（3）如圖3，在（2）的條件下，過點A作AN⊥GM于點N，若AN=14，CN-BG=8，求線段MN的長．
【考點】三角形綜合題．
【答案】（1）見解答；
（2）見解答；
（3）2．
（2）見解答；
（3）2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/10 8:0:9組卷：182引用：1難度：0.1
相似題
-
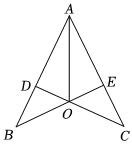1．如圖，AB=AC，CD⊥AB，BE⊥AC，垂足分別為D、E，BE、CD相交于點O，連接AO．
（1）不添加任何輔助線，寫出圖中所有的全等三角形．
（2）觀察猜想，AO是不是∠BAC的角平分線？如果認為是，請證明；如果認為不是，請說明理由．
（3）連接BC，如果OA=OB，求證：△ABC為等邊三角形．發布：2025/6/2 15:30:1組卷：19引用：1難度：0.3 -
2．[問題背景]
我們學習等邊三角形時，得到了直角三角形的一個性質：在直角三角形中，如果一個銳角等于30°，那么它所對的直角邊等于斜邊的一半．如圖①，在Rt△ABC中，∠ACB=90°，∠ABC=30°，則AC=AB．12
[探究結論]
小明同學對以上性質作了進一步探究．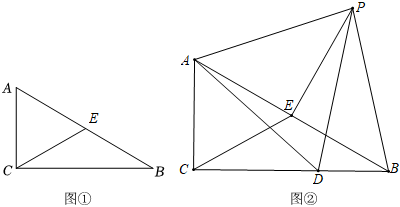
（1）如圖①，作AB邊上的中線CE，得到結論：△ACE是等邊三角形．請加以證明；
（2）如圖②，CE是△ABC的中線，D是邊BC上任意一點連接AD，作等邊三角形ADP，且點P在∠ACB的內部，連接BP，PE．求證：
①△ACD≌△AEP；
②PD=PB．發布：2025/6/2 15:30:1組卷：47引用：2難度：0.5 -
3．在Rt△ABC中，∠ACB=90°，CD⊥AB于點D，E為AB上一點（不與A，B重合）
（1）如圖1，若BC=BE，求證：CE平分∠ACD；
（2）如圖2，若AC=BC，過點B作BF⊥CE于點F，交CD于G．
①求證：AE=CG；
②當BC=BE時，BG與CF的數量關系是．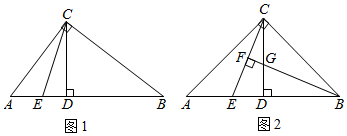
發布：2025/6/2 16:0:1組卷：409引用：2難度：0.4