《歌詞古體算題》記載了中國古代的一道在數學史上名揚中外的“勾股容圓”名題，其歌詞為：
十五為股八步勾，內容圓徑怎生求？
有人算得如斯妙，算學方為第一籌．
當中提出的數學問題是這樣的：已知直角三角形的兩直角邊邊長分別為15步，8步，試求其內切圓的直徑．
請你嘗試完成上述任務，如果時光倒流，看看你是否算得上古代中國的一流數學家．（溫馨提示：直角三角形的三邊存在這樣的數量關系：斜邊的平方等于兩直角邊的平方和．）

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：87引用：1難度：0.3

相似題

1．閱讀材料并解答問題：
與正三角形各邊都相切的圓叫做正三角形的內切圓，與正四邊形各邊都相切的圓叫做正四邊形的內切圓，…，與正n邊形各邊都相切的圓叫做正n邊形的內切圓，設正n（n≥3）邊形的面積為S_正n邊形，其內切圓的半徑為r,試探索正n邊形的面積．（結果可用三角函數表示）
如圖①，當n=3時，設AB切圓O于點C，連接OC，OA，OB，∴OC⊥AB，OA=OB，∴
∠
AOC
=
1
2
AOB
，AB=2BC．
在Rt△AOC中，∵
∠
AOC
=
1
2
?
360
°
3
=
60
°
，OC=r,∴AC=r?tan60°，AB=2r?tan60°，∴
S
△
OAB
=
1
2
?
r
?
2
rtan
60
°
=
r
2
tan
60
°
，∴S_正三角形=3S_△OAB=3r²?tan60°．
（1）如圖②，當n=4時，仿照（1）中的方法和過程可求得：S_正四邊形=
；
（2）如圖③，當n=5時，仿照（1）中的方法和過程求S_正五邊形；
（3）如圖④，根據以上探索過程，請直接寫出S_正n邊形=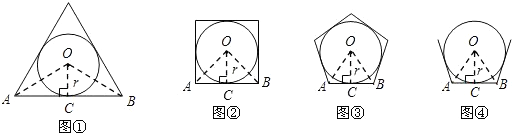
．
發布：2025/5/22 23:30:1組卷：216引用：6難度：0.5
解析
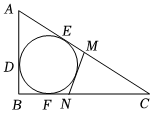2．如圖⊙O是△ABC的內切圓，切點分別是D，E，F，其中AB=6，BC=9，AC=11，若MN與⊙O相切與G點，與AC，BC相交于M，N點，則△CMN的周長等于
．
發布：2025/5/22 16:0:1組卷：459引用：5難度：0.5
解析
3．如圖，已知⊙O是△ABC的內切圓，∠C=90°，BO的延長線交AC于點D，若BC=4，CD=1，則⊙O的半徑長為
．
發布：2025/5/22 19:30:1組卷：667引用：3難度：0.5
解析

相關試卷

2．如圖⊙O是△ABC的內切圓，切點分別是D，E，F，其中AB=6，BC=9，AC=11，若MN與⊙O相切與G點，與AC，BC相交于M，N點，則△CMN的周長等于 ．