如圖，平面直角坐標(biāo)系中，直線AB分別交x軸正半軸于點(diǎn)A，交y軸正半軸于點(diǎn)B，且OA、OB（OA＜OB）的長是方程x2-12x+32=0的兩個(gè)根．
（1）求AB的值；
（2）已知點(diǎn)C是OB的中點(diǎn)，當(dāng)點(diǎn)P在射線BA上運(yùn)動到S△AOC=S△AOP時(shí)，求點(diǎn)P的坐標(biāo)．
（3）若點(diǎn)Q在線段AB上，平移直線OQ交x軸于點(diǎn)D，交y軸于點(diǎn)E．當(dāng)M（0，4），N（-4，0）時(shí)，是否存在點(diǎn)D，E使得以點(diǎn)D、E、M、N為頂點(diǎn)的四邊形是正方形？若存在，直接寫出點(diǎn)E的坐標(biāo)；若不存在，請說明理由．
【考點(diǎn)】四邊形綜合題．
【答案】（1）AB=4；
（2）P（2，4）；
（3）存在點(diǎn)D，E使得以點(diǎn)D、E、M、N為頂點(diǎn)的四邊形是正方形，理由見解答過程；E（0，-4）．
5
（2）P（2，4）；
（3）存在點(diǎn)D，E使得以點(diǎn)D、E、M、N為頂點(diǎn)的四邊形是正方形，理由見解答過程；E（0，-4）．
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/19 0:0:1組卷：47引用：3難度：0.5
相似題
-
1．如圖所示，四邊形ABCD為菱形，AD=5，sinB=，點(diǎn)E為邊AB上一動點(diǎn)（不與端點(diǎn)重合），△DEF與△DEA關(guān)于DE對稱．2425
（1）試求菱形ABCD的面積；
（2）若點(diǎn)D、B、F共線，求AE的長；
（3）點(diǎn)G為邊CD上一點(diǎn)，且CG=1，連接GF、BF，試求BF+2GF的最小值．發(fā)布：2025/6/10 3:30:1組卷：283引用：2難度：0.1 -
2．在平面直角坐標(biāo)系xOy中，對于點(diǎn)P（x1，y1），給出如下定義：當(dāng)點(diǎn)Q（x2，y2）滿足x1?x2=y1?y2時(shí)，稱點(diǎn)Q是點(diǎn)P的等積點(diǎn)．已知點(diǎn)P（1，2）．
（1）在Q1（2，1），Q2（-4，-1），Q3（8，2）中，點(diǎn)P的等積點(diǎn)是 ．
（2）點(diǎn)Q是P點(diǎn)的等積點(diǎn)，點(diǎn)C在x軸上，以O(shè)，P，Q，C為頂點(diǎn)的四邊形是平行四邊形，求點(diǎn)C的坐標(biāo)．
（3）已知點(diǎn)和點(diǎn)M（4，m），點(diǎn)N是以點(diǎn)M為中心，邊長為2且各邊與坐標(biāo)軸平行的正方形T上的任意一點(diǎn)，對于線段BN上的每一點(diǎn)A，在線段PB上都存在一個(gè)點(diǎn)R使得A為R的等積點(diǎn)，直接寫出m的取值范圍．B（1，12）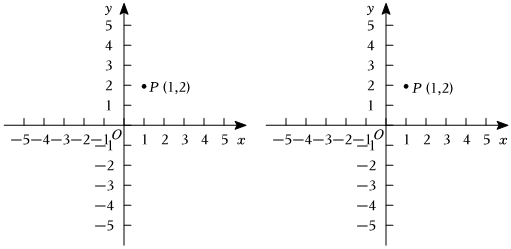
發(fā)布：2025/6/10 1:0:1組卷：129引用：1難度：0.9 -
3．感知：數(shù)學(xué)課上，老師給出了一個(gè)模型：如圖1，點(diǎn)A在直線DE上，且∠BDA=∠BAC=∠AEC=90°，像這種一條直線上的三個(gè)頂點(diǎn)含有三個(gè)相等的角的模型我們把它稱為“一線三等角“模型．
應(yīng)用：（1）如圖2，Rt△ABC中，∠ACB=90°，CB=CA，直線ED經(jīng)過點(diǎn)C，過A作AD⊥ED于點(diǎn)D，過B作BE⊥ED于點(diǎn)E．求證：△BEC≌△CDA．
（2）如圖3，在△ABC中，D是BC上一點(diǎn)，∠CAD=90°，AC=AD，∠DBA=∠DAB，AB=2，求點(diǎn)C到AB邊的距離．3
（3）如圖4，在?ABCD中，E為邊BC上的一點(diǎn)，F(xiàn)為邊AB上的一點(diǎn)．若∠DEF=∠B，AB=10，BE=6，求的值．EFDE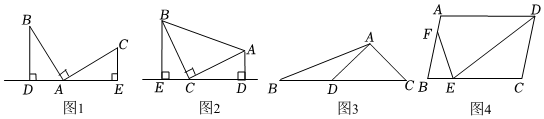
發(fā)布：2025/6/10 1:30:1組卷：2068引用：10難度：0.4