我們從生活實際發(fā)現(xiàn)，當一個直角三角形兩直角邊長確定時，斜邊長也就確定了．古代數(shù)學就已經(jīng)發(fā)現(xiàn)，在直角三角形中，若兩直角邊長為a,b,斜邊長為c,則a2+b2=c2．這就是著名的“勾股定理”（西方把它稱為“畢達哥拉斯定理”）．
（1）如圖，4個完全一樣的直角三角形（其兩直角邊長為a,b,斜邊長為c）與1個小正方形，不重疊無縫隙拼接成的正方形，請用這個圖驗證“勾股定理”．
（2）若直角三角形中兩直角邊的和a+b=4，斜邊c長為3，求直角三角形的面積．
【考點】勾股定理的證明．
【答案】（1）見解答；
（2）．
（2）
7
4
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：197引用：2難度：0.6
相似題
-
1．如圖，由弦圖變化得到，它是由八個全等的直角三角形拼接而成，圖中正方形ABCD，正方形EFGH，正方形MNKJ的面積分別記為S1，S2，S3，若EF=4，則S1+S2+S3的值是（ ）發(fā)布：2025/6/10 1:0:1組卷：403引用：2難度：0.4 -
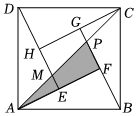2．我國古代數(shù)學家趙爽在注解《周髀算經(jīng)》時給出的“趙爽弦圖”，它是由4個全等的直角三角形與1個小正方形拼成的一個大正方形．如圖，若拼成的大正方形為正方形ABCD，面積為25，中間的小正方形為正方形EFGH，面積為3，連接AC，交BG于點P，交DE于點M，下列說法正確的是（ ）發(fā)布：2025/6/10 2:30:2組卷：169引用：4難度：0.4 -
3．如圖“趙爽弦圖”是由四個全等的直角三角形拼成的圖形，若大正方形的面積41，小正方形的面積是1，設直角三角形較長的直角邊為b,較短的直角邊為a,則a+b的值是（ ）發(fā)布：2025/6/10 0:30:1組卷：640引用：5難度：0.8
相關(guān)試卷