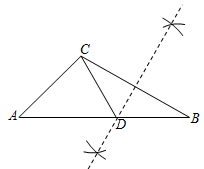
如圖，在△ABC中，∠A=45°，∠B=30°，尺規(guī)作圖如下：分別以點B、點C為圓心，大于12BC為半徑作弧，連接兩弧交點的直線交AB于點D，連接CD，則∠ACD的度數(shù)為（ ）
1
2
【考點】三角形內(nèi)角和定理．
【答案】D
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/7/12 8:0:9組卷：1512引用：10難度：0.9
相似題
-
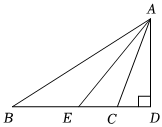1．如圖，在△ABC中，AD是BC邊上的高，AE平分∠BAC，∠B=30°，∠BCA=100°，則∠DAE的度數(shù)為 ．發(fā)布：2025/6/7 6:30:1組卷：49引用：2難度：0.5 -
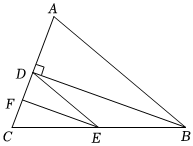2．如圖，在三角形ABC中，BD⊥AC于點D，BD平分∠ABC，∠CDE=∠A，EF平分∠CED，求證：EF⊥AC．
下面是小紅同學的部分推導過程，請你幫助他完善推導內(nèi)容和依據(jù)．
證明：∵∠CDE=∠A（已知），
∴DE∥AB （ ）．
∴∠CED=（ ）．
∵BD平分∠ABC，EF平分∠CED（已知），
∴∠CBD=∠CBA，∠CEF=12∠CED（ ）．12
∴∠CBD=∠CEF（等量代換）．
∴EF∥BD（ ）．
∴∠AFE=∠ADB （ ）．
∵BD⊥AC（已知），
∴∠ADB=90°（ ）．
∴∠AFE=∠ADB=90°（等量代換）．
∴EF⊥AC （ ）．發(fā)布：2025/6/7 9:30:1組卷：43引用：2難度：0.6 -
3．如圖，在△ABC中，∠BAC=90°，AD是高，BE是中線，CF是角平分線，CF交AD于點G，交BE于點H，下面說法正確的是（ ）
①△ABE的面積=△BCE的面積；②∠AFG=∠AGF；③∠FAG=2∠ACF；④BH=CH．發(fā)布：2025/6/7 7:30:1組卷：10766引用：48難度：0.3
相關(guān)試卷