妙樂寺塔又名妙樂寺真身舍利塔,位于河南省焦作市武陟縣,是我國現存最古老、規(guī)模最大、保存最為完整的五代大型磚塔.李明作為一名數學愛好者,想用自己學過的方法測量這座塔的高度.如圖,在該塔AB前有一棵古樹CD,兩者相距11.5m,李明在點E處測得樹的頂端C的仰角為35°,從點E出發(fā)沿EB方向前進9m到達G處,測得點C的仰角為45°(B、D、G、E在一條直線上),此時恰好看不到該建筑物的頂端A(A、C、H三點共線).已知李明的眼睛離地面1.7m(即EF=HG=1.7m).求該塔AB的高(結果精確到1m.參考數據:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70).
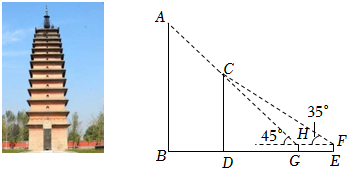
【考點】解直角三角形的應用-仰角俯角問題.
【答案】約為34m.
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網所有,未經書面同意,不得復制發(fā)布。
發(fā)布:2025/5/26 2:30:2組卷:108引用:1難度:0.6
相似題
-
 1.某“綜合與實踐”小組開展了測量本校旗桿高度的實踐活動.他們制訂了測量方案,并利用課余時間完成了實地測量.他們在該旗桿底部所在的平地上,選取兩個不同測點,分別測量了該旗桿頂端的仰角以及這兩個測點之間的距離.為了減小測量誤差,小組在測最仰角的度數以及兩個測點之間的距離時,都分別測量了兩次并取它們的平均值作為測量結果,測量數據如下表(不完整).
1.某“綜合與實踐”小組開展了測量本校旗桿高度的實踐活動.他們制訂了測量方案,并利用課余時間完成了實地測量.他們在該旗桿底部所在的平地上,選取兩個不同測點,分別測量了該旗桿頂端的仰角以及這兩個測點之間的距離.為了減小測量誤差,小組在測最仰角的度數以及兩個測點之間的距離時,都分別測量了兩次并取它們的平均值作為測量結果,測量數據如下表(不完整).
任務一:兩次測量,A,B之間的距離的平均值是 m.課題 測量旗桿的高度 成員 組長×××組員:×××,×××,××× 測量工具 測量角度的儀器、皮尺等 測量示意圖 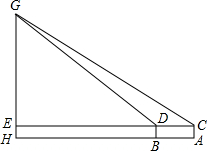
說明:線段GH表示學校旗桿,測量角度的儀器的高度AC=BD=1.5m,測點A,B與H在同一條水平直線上,A,B之間的距離可以直接測得,且點G,H,A,B,C,D都在同一豎直平面內.點C,D,E在同一條直線上,點E在GH上. 測量項目 第一次 第二次 平均值 測量數據 ∠GCE的度數 25.6° 25.8° 25.7° ∠GDE的度數 31.2° 30.8° 31° A,B之間的距離 5.4m 5.6m
任務二:根據以上測量結果,請你幫助該“綜合與實踐”小組求出學校旗桿GH的高度.
(參考數據:sin25.7°≈0.43,cos25.7°≈0.90,tan25°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
任務三:該“綜合與實踐”小組在制訂方案時,討論過利用物體在陽光下的影子測量旗桿的高度”的方案,但未被采納.你認為其原因可能是什么?發(fā)布:2025/5/26 3:30:1組卷:235引用:3難度:0.5 -
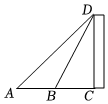 2.如圖,為測量建筑物CD的高度,在A點測得建筑物頂部D點的仰角為45°,再向建筑物CD前進30米到達B點,測得建筑物頂部D點的仰角為60°(A,B,C三點在一條直線上),則建筑物CD的高度為( )米.
2.如圖,為測量建筑物CD的高度,在A點測得建筑物頂部D點的仰角為45°,再向建筑物CD前進30米到達B點,測得建筑物頂部D點的仰角為60°(A,B,C三點在一條直線上),則建筑物CD的高度為( )米.A.15+15 3B.45+15 3C.15 -153D.45-15 3發(fā)布:2025/5/26 6:0:1組卷:214引用:3難度:0.7 -
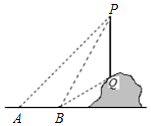 3.如圖,一根電線桿PQ直立在山坡上,從地面的點A看,測得桿頂端點A的仰角為45°,向前走6m到達點B,又測得桿頂段P和桿底端點Q的仰角分別為60°和30°.
3.如圖,一根電線桿PQ直立在山坡上,從地面的點A看,測得桿頂端點A的仰角為45°,向前走6m到達點B,又測得桿頂段P和桿底端點Q的仰角分別為60°和30°.
(1)求證:△BPQ是等腰三角形;
(2)求電線桿PQ的高度.(結果精確到1m)發(fā)布:2025/5/26 5:30:2組卷:165引用:3難度:0.5


