在矩形ABCD中，AB=CD=4，CB=DA=6，P為CD上的動點，Q為DA上的動點，∠QPR=90°且PQ=PR．
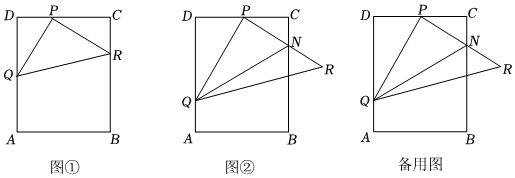
（1）如圖①，當點R在CB上時，求DQ+CR的值．
（2）如圖②，PR與CB相交于點N，連接QN，當QP平分∠DQN時，求證：S△QPN=S△DPQ+S△CPN．
（3）在（2）的前提下，連接CR，當CR=2PD時，求sin∠NQR的值．
2
【考點】四邊形綜合題．
【答案】（1）4；
（2）證明見解析；
（3）．
（2）證明見解析；
（3）
10
10
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：92引用：2難度：0.4
相似題
-
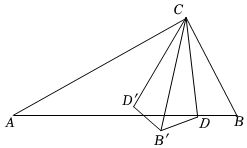1．如圖，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=1．動點D從點B出發沿BA方向以每秒1個單位長度的速度向終點A運動．當點D與點B不重合時，連結CD，作點B關于CD的對稱點B′，連結DB′，CB′；再作點D關于CB'的對稱點D′，連結B'D'，CD'．設點D運動時間為t秒．
（1）AB的長為 ．
（2）當四邊形CDB'D'為中心對稱圖形時，求t的值．
（3）當∠ACB'＜30°時，求t的取值范圍．
（4）當點D'在△ABC的一邊所在的直線上時，直接寫出t的值．發布：2025/5/26 6:0:1組卷：186引用：1難度：0.1 -
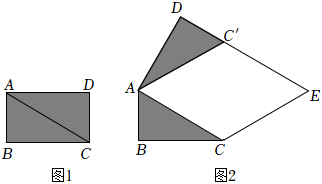2．如圖①，矩形紙片ABCD的邊AB=1，BC=2，將矩形紙片ABCD沿對角線AC剪開，得到△ABC和△ACD．如圖②，將△ACD繞點A逆時針方向旋轉∠α，（0°＜α＜360°，且α≠180°）得到△AC'D，過點C作AC'的平行線，過點C'作AC的平行線，兩直線交于點E．
（1）求證：四邊形ACEC′是菱形．
（2）當∠α=90°時，求四邊形ACEC'的面積．
（3）當四邊形ACEC'有一個角是45度時，直接寫出線段DC'掃過的面積．發布：2025/5/26 7:0:2組卷：92引用：1難度：0.3 -
3．在正方形ABCD中，對角線AC、BD相交于點O，F是正方形ABCD內一點，∠BFC=90°，將△BFC繞點C按順時針方向旋轉一定角度得到△DEC，點B、F的對應點分別為點D、E，則直線EF經過點O．
【方法感知】如圖①，當點F在△AOB內時，過點D作DG⊥DE交EF于點G，則∠DGE的大小為 度，DE、OE、OF的數量關系為 ．
【類比遷移】如圖②，當點F在△COD內時，試判斷DE、OE、OF之間的數量關系，并說明理由．
【拓展應用】如圖③，將正方形ABCD改為菱形，對角線AC、BD相交于點O，F是△COD內一點，∠BFC=90°．若將△BFC繞點C按順時針方向旋轉60°得到△DEC，點B、F的對應點分別為點D、E．若DE=2，則OE+OF=．2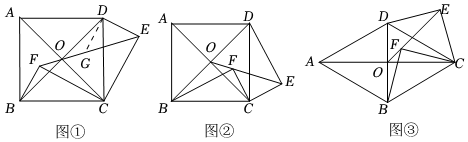
發布：2025/5/26 7:30:2組卷：160引用：1難度：0.3