如圖1，C為x軸正半軸上一動點，A（0，a），B（b,0），且a,b滿足a-6+|b+8|=0，AB=10．
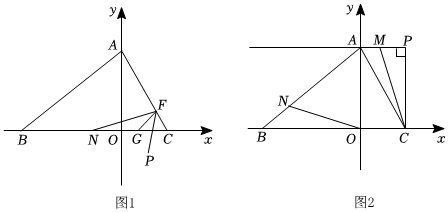
（1）求△ABO的面積；
（2）如圖1，若∠ACB=60°，G為線段BC上的動點，過點G作GF∥AB，交AC于點F，FP平分∠GFC，FN平分∠AFP交x軸于點N，記∠FNB=a,用a表示∠BAC的大小；
（3）如圖2，若P（3，6），PC⊥x軸于點C，點M從點P出發，在射線PA上運動，同時另一動點N從點B出發向點A運動，到點A時兩點停止運動，M，N的速度分別為2個單位長度/秒，3個單位長度/秒，當S△MAC=13S△BON時，求運動的時間t的值．
a
-
6
+
|
b
+
8
|
=
0
S
△
MAC
=
1
3
S
△
BON
【考點】三角形綜合題．
【答案】（1）24；
（2）4α-600°；
（3）t1=，t2=．
（2）4α-600°；
（3）t1=
15
14
5
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/7 8:0:9組卷：87引用：1難度：0.1
相似題
-
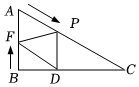1．如圖，在Rt△ABC?中，∠ABC=90°，∠C=30°，AB=9cm?，動點P?從點A?開始以2cm/s?的速度向點C?運動，動點F?從點B?開始以1cm/s?的速度向點A?運動，兩點同時運動，同時停止，運動時間為t（s）?．
（1）當t?為何值時，△PAF?是等邊三角形？
（2）當t?為何值時，△PAF?是直角三角形？
（3）過點P?作PD⊥BC?于點D?，連接DF?．
①求證：四邊形AFDP?是平行四邊形；
②當t?為何值時，△PDC?的面積是△ABC?面積的一半．發布：2025/5/24 1:0:1組卷：283引用：3難度：0.3 -
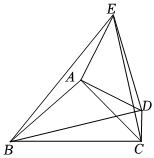2．如圖，在△ABC中，AB=AC=3，∠BAC=90°，點D為一個動點，且點D到點C的距離為1，連接CD，AD，作EA⊥AD，使AE=AD．
（1）求證：△ADB≌△AEC；
（2）求證：BD⊥EC；
（3）直接寫出BD最大和最小值；
（4）點D在直線AC上時，求BD的長．發布：2025/5/23 21:0:1組卷：103引用：2難度：0.4 -
3．在一次數學興趣小組活動中，小明將兩個形狀相同，大小不同的三角板AOB和三角板DEB放置在平面直角坐標系中，點O（0，0），A（0，3），∠ABO=30°，BE=3．
（Ⅰ）如圖①，求點D的坐標；
（Ⅱ）如圖②，小明同學將三角板DEB繞點B按順時針方向旋轉一周．
①若點O，E，D在同一條直線上，求點D到x軸的距離；
②連接DO，取DO的中點G，在旋轉過程中，點G到直線AB的距離的最大值是 （直接寫出結果即可）．發布：2025/5/24 1:0:1組卷：573引用：2難度：0.3