如圖1,已知∠AOC=m°,∠BOC=n°且m、n滿足等式|3m-420|+(2n-40)2=0,射線OP從OB處繞點O以4度/秒的速度逆時針旋轉.
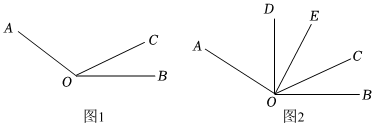
(1)試求∠AOB的度數;
(2)如圖1,當射線OP從OB處繞點O開始逆時針旋轉,同時射線OQ從OA處以1度/秒的速度繞點O順時針旋轉,設時間為t(0<t<40),當他們旋轉多少秒時,使得∠POQ=10°?
(3)如圖2,若射線OD為∠AOC的平分線,當射線OP從OB處繞點O開始逆時針旋轉,同時射線OT從射線OD處以x度/秒的速度繞點O順時針旋轉,使得這兩條射線重合于射線OE處(OE在∠DOC的內部)時,且∠COE∠DOE+∠BOC=45,試求x.
∠
COE
∠
DOE
+
∠
BOC
4
5
【答案】(1)160°;(2)30秒或34秒;(3)2.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/10/19 0:0:1組卷:353引用:1難度:0.4
相似題
-
1.某校組織生活小常識競賽,共設20道選擇題,各題分值相同,每題必答.如表記錄了其中4個參賽者的得分情況.
(1)參賽者E說他答錯了10道題,得50分.你認為可能嗎?請說明理由.參賽者 答對題數 答錯題數 得分 A 20 0 100 B 2 88 C 64 D 10 40
(2)補全表格,并寫出你的計算過程.發布:2025/6/2 21:30:9組卷:88引用:1難度:0.6 -
2.閱讀理解
絕對值是基本而重要的代數概念,是“距離”這一幾何量的代數表示,教材給出的定義是:一般地,數軸上表示數a的點與原點的距離叫做數a的絕對值,記作|a|.如果對這個定義作進一步研究,我們會發現:數軸上表示數a的點A與表示數b的點B之間的距離可以記作|a-b|,即:AB=|a-b|,比如:在數軸上,點A對應的數是2,點B對應的數是5,則點A與點B之間的距離AB=|2-5|=3.
嘗試練習
(1)在同一數軸上,點A對應的數是-2,點B對應的數是5,點P對應的數是x.
①AB=;
②若AP=1,即|x+2|=1,則x=;
③若|x+2|+|x-5|取最小值時,即AP+PB取最小值,求這個最小值.
拓展運用
(2)在同一數軸上,點A對應的數是-2,點B對應的數是5,若點P從點A出發,以每秒1個單位長度的速度沿數軸向右移動,同時,點Q從點B出發,以每秒2個單位長度的速度沿數軸向左移動,點Q到達點A后立即返回并沿數軸向右移動(點P到達點B后,P與Q均停止運動).設點P、Q移動的時間為t(秒).
①在0<t≤3.5范圍內,t為何值時,點P與點Q相遇?
②在3.5<1≤7范圍內,t為何值時,點P與點Q相距1個單位長度?發布:2025/6/2 22:0:1組卷:167引用:1難度:0.4 -
3.模型與應用
數學模型在數學中,可以用一條直線上的點表示數,這條直線叫做數軸.用數軸上的點表示數對數學的發展起了重要作用,借助圖直觀地表示很多與數相關的問題,體現了數形結合的思想方法.
問題解決如圖1,在數軸上,點A和點B表示的有理數分別為-2和4,點P、點Q為線段AB上兩點,點Q在點P右側且PQ=1對應的數為x,AP=3BQ,求此時x的值.
形成觀念如圖2,某地的高速口與動車口水平距離為1千米,同向平行行駛的轎車和動車在各自卡口同時出發.已知普通家庭轎車的長度是4米,行駛速度為120千米/小時;8組編的動車長度為266米,行駛速度為200千米/小時.求動車車頭追上轎車車尾到動車車尾離開轎車車頭需要多少秒? 發布:2025/6/2 22:0:1組卷:284引用:1難度:0.5
發布:2025/6/2 22:0:1組卷:284引用:1難度:0.5


