請觀察下列算式，找出規律并填空
①11×2=1-12，②11×3=12×（1-13），③11×4=13×（1-14），④11×5=14×（1-15），…
則第10個算式是11×1111×11=110×（1-111）110×（1-111），第n個算式為11×（n+1）11×（n+1）=1n×（1-1n+1）1n×（1-1n+1）．
從以上規律中你可得到一些啟示嗎？根據你得到的啟示，試解答下題：若有理數a、b滿足|a-1|+（b-3）2=0，求1ab+1（a+2）（b+2）+1（a+4）（b+4）+…+1（a+100）（b+100）的值．
1
1
×
2
1
2
1
1
×
3
1
2
1
3
1
1
×
4
1
3
1
4
1
1
×
5
1
4
1
5
1
1
×
11
1
1
×
11
1
10
1
11
1
10
1
11
1
1
×
（
n
+
1
）
1
1
×
（
n
+
1
）
1
n
×
1
n
+
1
1
n
×
1
n
+
1
1
ab
1
（
a
+
2
）
（
b
+
2
）
1
（
a
+
4
）
（
b
+
4
）
1
（
a
+
100
）
（
b
+
100
）
【答案】；×（1-）；；（1-）
1
1
×
11
1
10
1
11
1
1
×
（
n
+
1
）
1
n
×
1
n
+
1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1149引用：10難度：0.1
相似題
-
1．定義一種對正整數n的“F”運算：①當n為奇數時，F（n）=3n+1；②當n為偶數時，F（n）=
（其中k是使F（n）為奇數的正整數）……，兩種運算交替重復進行，例如，取n=24，則：n2k
若n=13，則第2020次“F”運算的結果是（ ）發布：2025/6/17 2:30:1組卷：970引用：5難度：0.6 -
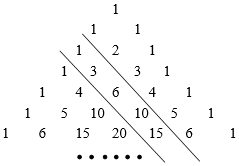2．如圖被稱為“楊輝三角”或“賈憲三角”．其規律是：從第三行起，每行兩端的數都是“1”，其余各數都等于該數“兩肩”上的數之和．表中兩平行線之間的一列數：1，3，6，10，15，…，我們把第一個數記為a1，第二個數記為a2，第三個數記為a3，…，第n個數記為an，則a6+a10的值為（ ）發布：2025/6/17 3:0:1組卷：480引用：2難度：0.6 -
3．觀察下列算式：31=3，32=9，33=27，34=81，35=243，36=729，37=2187，…，根據上述算式中的規律，你認為31+32+33+…+32020+32021的末位數字是 ．
發布：2025/6/16 23:30:1組卷：293引用：2難度：0.5