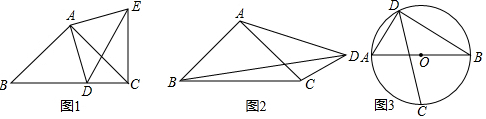
如圖1：在Rt△ABC中，AB=AC，D為BC邊上一點（不與點B，C重合），試探索AD，BD，CD之間滿足的等量關系，并證明你的結論．
小明同學的思路是這樣的：將線段AD繞點A逆時針旋轉90°，得到線段AE，連接EC，DE．繼續推理就可以使問題得到解決．
（1）請根據小明的思路，試探索線段AD，BD，CD之間滿足的等量關系，并證明你的結論；
（2）如圖2，在Rt△ABC中，AB=AC，D為△ABC外的一點，且∠ADC=45°，線段AD，BD，CD之間滿足的等量關系又是如何的，請證明你的結論；
（3）如圖3，已知AB是⊙O的直徑，點C，D是⊙O上的點，且∠ADC=45°．
①若AD=6，BD=8，求弦CD的長為7272；
②若AD+BD=14，求AD?（BD+22CD）的最大值，并求出此時⊙O的半徑．
2
2
AD
?
（
BD
+
2
2
CD
）
【考點】圓的綜合題．
【答案】7
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/30 3:0:9組卷：583引用：3難度：0.1
相似題
-
1．已知△ABC內接于⊙O，D是弧AC上一點，連接BD、AD，BD交AC于點M，∠BMC=∠BAD．
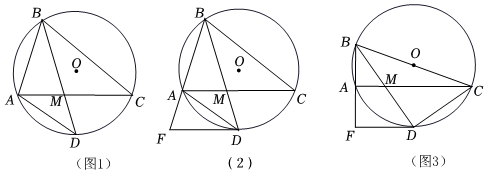
（1）如圖1，求證：BD平分∠ABC；
（2）如圖2，過點D作⊙O的切線，交BA的延長線于點F，求證：DF∥AC；
（3）如圖3，在（2）的條件下，BC是⊙O的直徑，連接DC，AM=1，DC=，求四邊形BFDC的面積．6發布：2025/5/25 21:0:1組卷：147引用：1難度：0.4 -
2．如圖，Rt△ABC中，AB=AC，∠BAC=90°，BC=6cm,點M，N是邊BC上的兩個動點，點M從點B出發沿著BC以每秒1cm的速度向終點C運動；點N同時從點C出發沿著CB以每秒2cm的速度向終點B運動．設運動時間為t秒．
（1）當t=1時，求△AMN的面積．
（2）當t為何值時，∠MAN=45°．
（3）當以MN為直徑的圓與△AMN的邊有且只有三個公共點時，請直接寫出t的取值范圍．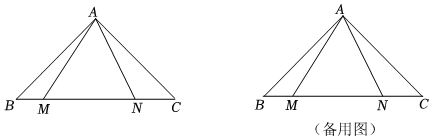
發布：2025/5/26 0:0:1組卷：335引用：2難度：0.3 -
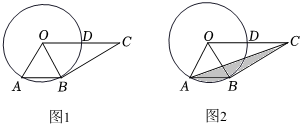3．如圖，點C為⊙O外一點，BC切⊙O于點B，弦AB∥OC，OC交⊙O于D．
（1）如圖1，連接BD，當∠AOB=度時，四邊形OABD是菱形；
（2）在（1）的條件下，
①試探究AB與BC的數量關系，并說明理由；
②如圖2，連接AC，若⊙O的半徑為2，陰影部分的面積為 （結果保留π）．發布：2025/5/25 21:30:1組卷：54引用：1難度：0.4