下面是小林設計的“利用直角三角形作矩形”的尺規作圖過程．
已知：在Rt△ABC中，∠ABC=90°．
求作：矩形ABCD．
作法：如圖②，
①分別以點A、C為圓心，大于12AC長為半徑作弧，兩弧相交于點E、F；
②作直線EF，直線EF交AC于點O；
③作射線BO，在BO上截取OD，使得OD=OB；
④連接AD，CD．
所以四邊形ABCD就是所求的矩形．
根據小林設計的尺規作圖過程．
（1）使用直尺和圓規，補全圖形；（保留作圖痕跡）
（2）完成下面的證明．
證明：OA=OCOC，OD=OB，
∴四邊形ABCD為平行四邊形（ 對角線互相平分的四邊形為平行四邊形對角線互相平分的四邊形為平行四邊形）（填推理依據）．
又∵∠ABC=90°，
∴四邊形ABCD為矩形（ 有一個內角為90°的平行四邊形為矩形有一個內角為90°的平行四邊形為矩形）（填推理依據）．
1
2
AC
【答案】OC；對角線互相平分的四邊形為平行四邊形；有一個內角為90°的平行四邊形為矩形
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/23 20:19:40組卷：66引用：2難度：0.5
相似題
-
1．如圖，在△ABC中，∠B=∠C=30°．
（1）在圖1中求作⊙O，使⊙O經過B、C兩點，且與直線AB、AC相切．（尺規作圖，保留作圖痕跡，不必寫作法）
（2）已知BC=6，則⊙O的半徑=．（如需畫草圖，請使用圖2）發布：2025/5/24 4:30:1組卷：309引用：2難度：0.5 -
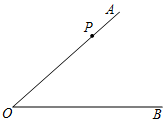2．如圖，點P是∠AOB邊OA上的一點，按要求作（畫）圖，并填空：
（1）用圓規和直尺作線段OP的垂直平分線，交OA、OB分別于點M、N；
（2）過點M畫出表示點M到直線OB距離的線段MH；
（3）點N到直線OB的距離的大小為；發布：2025/5/24 5:0:1組卷：63引用：3難度：0.7 -
3．已知：線段AB．
求作：Rt△ABC，使得∠BAC=90°，∠C=30°．
作法：
①分別以點A和點B為圓心，AB長為半徑作弧，兩弧交于點D；
②連接BD，在BD的延長線上截取DC=BD；
③連接AC．
則△ABC為所求作的三角形．
（1）使用直尺和圓規，依作法補全圖形（保留作圖痕跡）；
（2）完成下面的證明．
證明：連接AD．
∵AB=AD=BD，
∴△ABD為等邊三角形（ ）．（填推理的依據）
∴∠B=∠ADB=60°．
∵CD=BD，
∴AD=CD
∴∠DAC=（ ）．（填推理的依據）
∴∠ADB=∠C+∠DAC=60°．
∴∠C=30°．
在△ABC中，
∠BAC=180°-（∠B+∠C）=90°．發布：2025/5/24 4:30:1組卷：206引用：6難度：0.5